
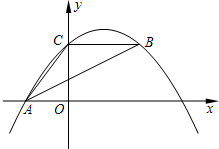
 如图,抛物线y=(m-1)x2+(5-5m)x+4经过△ABC的三个顶点,点A在x轴上,点C在y轴上,B与C是抛物线的对称点,AB平分∠CAO.
如图,抛物线y=(m-1)x2+(5-5m)x+4经过△ABC的三个顶点,点A在x轴上,点C在y轴上,B与C是抛物线的对称点,AB平分∠CAO.分析 (1)由抛物线y=(m-1)x2+(5-5m)x+4,确定点C(0,4),利用抛物线对称轴为x=-$\frac{5-5m}{2(m-1)}$=$\frac{5}{2}$,得到点B(5,4),BC=5,根据BC关于对称轴对称,即BC∥x轴,得到∠CBA=∠OAB,再利用AB平分∠CAO,可得∠CBA=∠CAB,AC=BC=5,在Rt△AOC中,利用勾股定理求出AO=3,确定点A(-3,0),代入抛物线y=(m-1)x2+(5-5m)x+4,解得:m=$\frac{5}{6}$,即可确定抛物线的解析式;
(2)如图,从P作x轴垂线,交BC于点E,交AB于Q,交x轴于点F;则AF⊥PF,设长度为AF=h1;则BE⊥PQ,设BE长度为h2,显然h1+h2为A、B横坐标的差,为8,利用待定系数法求出直线AB解析式为y=$\frac{1}{2}x+\frac{3}{2}$,因为P在抛物线上,所以设P(m,-$\frac{1}{6}{m}^{2}+\frac{5}{6}m$+4),Q(m,$\frac{1}{2}m+\frac{3}{2}$),则PQ=-$\frac{1}{6}{m}^{2}+\frac{5}{6}m$+4-($\frac{1}{2}m+\frac{3}{2}$)=-$\frac{1}{6}{m}^{2}+\frac{1}{3}m+\frac{5}{2}$,分别表示出${S}_{△APQ}=\frac{1}{2}•PQ•{h}_{1}$,${S}_{△BPQ}=\frac{1}{2}•PQ•{h}_{2}$,则S△PAB=S△APQ+S△BPQ=$\frac{1}{2}•PQ•({h}_{1}+{h}_{2})$=$-\frac{2}{3}{m}^{2}+\frac{4}{3}m+10$=-$\frac{2}{3}(m-1)^{2}+\frac{32}{3}$,根据二次函数的性质,可得当m=-$\frac{b}{2a}$=1时,S△PAB最大,代入P点横坐标m=1,n=-$\frac{1}{6}+\frac{5}{6}$+4=$\frac{14}{3}$,即可得到P(-1,$\frac{14}{3}$).
解答 解:(1)抛物线y=(m-1)x2+(5-5m)x+4,
当x=0,则y=4.
因此C(0,4)
抛物线对称轴为x=-$\frac{5-5m}{2(m-1)}$=$\frac{5}{2}$,
∵B与C是抛物线的对称点,
∴B(5,4),BC=5,
∵BC关于对称轴对称,
∴BC∥x轴,
∴∠CBA=∠OAB
∵AB平分∠CAO,
∴∠CAB=∠OAB,
∴∠CBA=∠CAB,AC=BC=5,
在Rt△AOC中,AC=5,OC=4,则AO=$\sqrt{A{C}^{2}-O{C}^{2}}$=3
∴A(-3,0),
抛物线y=(m-1)x2+(5-5m)x+4,
代入A点坐标,得:9(m-1)-3(5-5m)+4=0
解得:m=$\frac{5}{6}$
抛物线解析式为y=-$\frac{1}{6}{x}^{2}$+$\frac{5}{6}x$+4
(2)如图,从P作x轴垂线,交BC于点E,交AB于Q,交x轴于点F;则AF⊥PF,设长度为AF=h1;则BE⊥PQ,设BE长度为h2,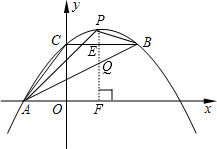
显然h1+h2为A、B横坐标的差,为8,
设直线AB解析式为y=kx+b
代入A、B坐标,可得:$\left\{\begin{array}{l}{-3k+b=0}\\{5k+b=4}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$
所以y=$\frac{1}{2}x+\frac{3}{2}$,
因为P在抛物线上,所以设P(m,-$\frac{1}{6}{m}^{2}+\frac{5}{6}m$+4),Q(m,$\frac{1}{2}m+\frac{3}{2}$),
则PQ=-$\frac{1}{6}{m}^{2}+\frac{5}{6}m$+4-($\frac{1}{2}m+\frac{3}{2}$)=-$\frac{1}{6}{m}^{2}+\frac{1}{3}m+\frac{5}{2}$,
∵${S}_{△APQ}=\frac{1}{2}•PQ•{h}_{1}$,${S}_{△BPQ}=\frac{1}{2}•PQ•{h}_{2}$,
∴S△PAB=S△APQ+S△BPQ=$\frac{1}{2}•PQ•({h}_{1}+{h}_{2})$=$-\frac{2}{3}{m}^{2}+\frac{4}{3}m+10$=-$\frac{2}{3}(m-1)^{2}+\frac{32}{3}$,
当m=-$\frac{b}{2a}$=1时,S△PAB最大
代入P点横坐标m=1,n=-$\frac{1}{6}+\frac{5}{6}$+4=$\frac{14}{3}$
所以P(1,$\frac{14}{3}$).
点评 本题考查了二次函数的性质、勾股定理、平行线的性质、待定系数法求函数的解析式以及角平分线,解决本题的关键是求出二次函数的解析式,利用二次函数的性质解决最值的问题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两组对边分别平行的四边形是平行四边形 | |
| B. | 正三角形是特殊的三角形 | |
| C. | 在同一平面内三条线段首尾相连得到的图形是三角形 | |
| D. | 含有未知数的等式叫做方程 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某次青年歌手大赛中,设置了基本知识问答题,答对一题得5分,答错或不答得0分,40名歌手的答对题数统计结果如图所示:求这批选手得分的中位数、众数和平均数.
某次青年歌手大赛中,设置了基本知识问答题,答对一题得5分,答错或不答得0分,40名歌手的答对题数统计结果如图所示:求这批选手得分的中位数、众数和平均数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>$\frac{3}{2}$ | B. | x≥$\frac{3}{2}$ | C. | x>-$\frac{3}{2}$ | D. | x≥-$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4、1 | B. | -4、1 | C. | -4、-1 | D. | 4、-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com