
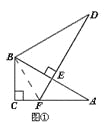
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.

【答案】(1)通过三角形全等来分析CF=EF,进而代换求角(2)图二(3)不成立,正确的结论是AF-EF=DE
【解析】试题分析:(1)利用旋转的性质以及全等三角形的判定得出Rt△BCF≌Rt△BEF,进而得出答案;
(2)利用旋转的性质以及全等三角形的判定得出Rt△BCF≌Rt△BEF,进而得出答案;
(3)利用旋转的性质以及全等三角形的判定得出Rt△BCF≌Rt△BEF,进而得出答案.
试题解析:(1)如图①所示,连接BF,
∵BC=BE,
在Rt△BCF和Rt△BEF中
![]()
∴Rt△BCF≌Rt△BEF(HL),
∴EF=CF,
∴AF+EF=AC=DE;
(2)如图②所示:
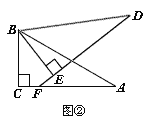
延长DE交AC与点F,连接BF,
在Rt△BCF和Rt△BEF中
![]()
∴Rt△BCF≌Rt△BEF(HL),
∴EF=CF,
∴AF+EF=AC=DE;
(3)如图③所示:
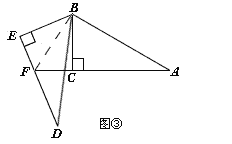
连接BF,
在Rt△BCF和Rt△BEF中
![]()
∴Rt△BCF≌Rt△BEF(HL),
∴EF=CF,
∴AF-FC=AC=DE,
∴AF-EF=DE.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,图象(折线OEFPMN)描述了某汽车在行驶过程中速度与时间的函数关系,下列说法中错误的是( )

A. 第3分时汽车的速度是40千米/时
B. 第12分时汽车的速度是0千米/时
C. 从第3分到第6分,汽车行驶了120千米
D. 从第9分到第12分,汽车的速度从60千米/时减少到0千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
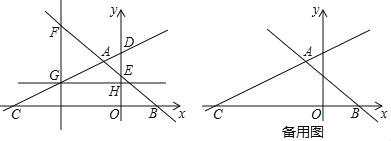
【题目】如图,在平面直角坐标系中,直线AB:y=﹣![]() x+
x+![]() 与直线AC:y=
与直线AC:y=![]() +8交于点A,直线AB分别交x轴、y轴于B、E,直线AC分别交x轴、y轴于点C、D.
+8交于点A,直线AB分别交x轴、y轴于B、E,直线AC分别交x轴、y轴于点C、D.
(1)求点A的坐标;
(2)在y轴左侧作直线FG∥y轴,分别交直线AB、直线AC于点F、G,当FG=3DE时,过点G作直线GH⊥y轴于点H,在直线GH上找一点P,使|PF﹣PO|的值最大,求出P点的坐标及|PF﹣PO|的最大值;
(3)将一个45°角的顶点Q放在x轴上,使其角的一边经过A点,另一边交直线AC于点R,当△AQR为等腰直角三角形时,请直接写出点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
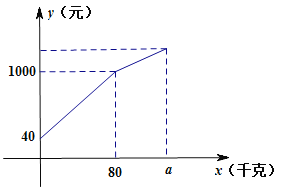
【题目】一果农带了若干千克自产的苹果进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又半价售完剩下的苹果.售出苹果千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)果农自带的零钱是多少?
(2)降价前他每千克苹果出售的价格是多少?
(3)降价售完剩余苹果后,这时他手中的钱(含备用零钱)是1120元,问果农一共带了多少千克苹果?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长度为50m .设饲养室为长为x(m),占地面积为![]() .
.
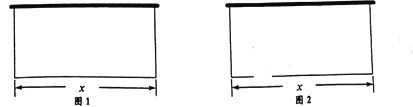
(1)如图![]() ,问饲养室为长x为多少时,占地面积y 最大?
,问饲养室为长x为多少时,占地面积y 最大?
(2)如图![]() ,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.
,现要求在图中所示位置留2m的门,且仍使饲养室占地面积最大.小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅计划购买12张餐桌和一批椅子(不少于12把),现从甲、乙两商场了解到同一型号的餐桌报价都为每张200元,餐椅报价都为每把50元.甲商场规定:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌、餐椅均按报价的八五折销售,那么,什么情况下到甲商场购买更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
在平面直角坐标系中,二元一次方程x-y=0的一个解![]() 可以用一个点(1,1)表示,二元一次方程有无数个解,以方程x-y=0的解为坐标的点的全体叫作方程x-y=0的图象。一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程x-y=0的图象称为直线x-y=0。
可以用一个点(1,1)表示,二元一次方程有无数个解,以方程x-y=0的解为坐标的点的全体叫作方程x-y=0的图象。一般地,在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,我们可以把方程x-y=0的图象称为直线x-y=0。
直线x-y=0把坐标平面分成直线上方区域,直线上,直线下方区域三部分,如果点M(x0,y0)的坐标满足不等式x-y≤0,那么点M(x0,y0)就在直线x-y=0的上方区域内。特别地,x=k(k为常数)表示横坐标为k的点的全体组成的一条直线,y=m(m为常数)表示纵坐标为m的点的全体组成的一条直线。
请根据以上材料,探索完成以下问题:
(1)已知点A(2,1)、B(![]() ,
,![]() )、C(
)、C(![]() ,
,![]() )、D(4,
)、D(4,![]() ),其中在直线3x-2y=4上的点有 ;请再写出直线3x-2y=4上一个点的坐标 ;
),其中在直线3x-2y=4上的点有 ;请再写出直线3x-2y=4上一个点的坐标 ;
(2)已知点P(x,y)的坐标满足不等式组![]() ,则所有的点P组成的图形的面积是 ;
,则所有的点P组成的图形的面积是 ;
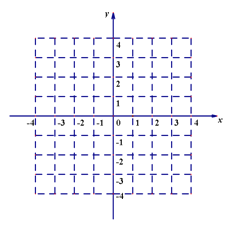
(3)已知点P(x,y)的坐标满足不等式组 ,请在平面直角坐标系中画出所有的点P组成的图形(涂上阴影),并直接写出上述图形的面积 。
,请在平面直角坐标系中画出所有的点P组成的图形(涂上阴影),并直接写出上述图形的面积 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,(k为常数,k≠1).
,(k为常数,k≠1).
(1)若点A(1,2)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一分支上,y随x的增大而增大,求k的取值范围;
(3)若k=13,试判断点B(3,4),C(2,5)是否在这个函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC切⊙O于点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.

(1)试判断∠CBD与∠CEB是否相等,并证明你的结论;
(2)求证:![]() ;
;
(3)若BC=![]() AB,求tan∠CDF的值.
AB,求tan∠CDF的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com