
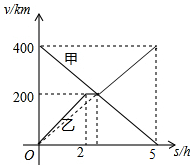
 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲,乙两车距B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲,乙两车距B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:分析 (1)根据速度=路程÷时间即可算出甲车的速度,再根据时间=路程÷速度可算出两车相遇的时间,减去2后即可得出结论;
(2)设乙车与甲车相遇后y乙关于x的函数解析式为y乙=kx+b(k≠0),观察图形找出点的坐标利用待定系数法即可得出结论;
(3)根据函数图象结合待定系数法求出y甲,y乙与x之间的函数解析式,分三段求出两车相距80km的时间,此题得解.
解答 解:(1)甲车的速度为:400÷5=80(km/h),
甲、乙两车相遇的时间为:(400-200)÷80=2.5(h),
乙车休息时间为:2.5-2=0.5(h).
故答案为:80;0.5.
(2)设乙车与甲车相遇后y乙关于x的函数解析式为y乙=kx+b(k≠0),
将点(2.5,200)、(5,400)代入y乙=kx+b中,得:
$\left\{\begin{array}{l}{200=2.5k+b}\\{400=5k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=80}\\{b=0}\end{array}\right.$.
∴乙车与甲车相遇后y乙关于x的函数解析式为y乙=80x(2.5≤x≤5).
(3)当0≤x≤2时,乙车的速度为:200÷2=100(km/h),
∴y乙=100x;
当2≤x≤2.5时,y乙=200.
∴y乙=$\left\{\begin{array}{l}{100x(0≤x≤2)}\\{200(2≤x≤2.5)}\\{80x(2.5≤x≤5)}\end{array}\right.$.
设y甲与x之间的函数解析式为y甲=mx+n(m≠0),
将(0,400)、(5,0)代入y甲=mx+n中,得:
$\left\{\begin{array}{l}{n=400}\\{5m+n=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-80}\\{n=400}\end{array}\right.$,
∴y甲与x之间的函数解析式为y甲=-80x+400(0≤x≤5).
当0≤x≤2时,令y甲-y乙=80,即-80x+400-100x=80,
解得:x=$\frac{16}{9}$;
当2≤x≤2.5时,令y甲-y乙=80,即-80x+400-200=80,
解得:x=$\frac{3}{2}$(舍去);
当2.5≤x≤5时,令y乙-y甲=80,即80x-(-80x+400)=80,
解得:x=3.
综上可知:当甲车出发$\frac{16}{9}$小时或3小时后,两车相距80km.
点评 本题考查了一次函数的应用以及待定系数法求一次函数解析式,观察图形找出点的坐标利用待定系数法求出函数解析式是解题的关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
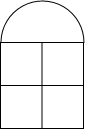 如图,是一扇窗户的设计图,它由四个小正方形及一个半圆组成,已知半圆的半径为a米.(结果保留π)
如图,是一扇窗户的设计图,它由四个小正方形及一个半圆组成,已知半圆的半径为a米.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
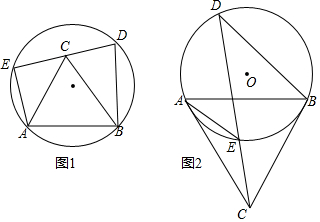
 如图,平行四边形ABCD中,点E为DC上一点,连接AE,F为AE上一点,连接BF,∠AFB=∠EFB,G在BF上,连接AG、EG,FG平分∠AGE.
如图,平行四边形ABCD中,点E为DC上一点,连接AE,F为AE上一点,连接BF,∠AFB=∠EFB,G在BF上,连接AG、EG,FG平分∠AGE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知平行四边形ABCD中,点E是对角线AC上的一点,且满足AE:EC=1:3,连接BE并延长,交AD于点G,交CD的延长线于点F,求AG:GD的值.
如图,已知平行四边形ABCD中,点E是对角线AC上的一点,且满足AE:EC=1:3,连接BE并延长,交AD于点G,交CD的延长线于点F,求AG:GD的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com