
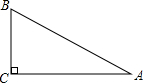
 如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.
如图,台风过后,琼岛小学的旗杆在B处折断,旗杆顶部A落在离旗杆底部8米处,已知旗杆长16米,则旗杆是在离底部6米处断裂.  每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
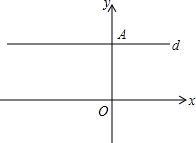 如图,在平面直角坐标系中,点O为坐标原点,A(0,a),B(b,0),a与b为方程组$\left\{\begin{array}{l}{4a+3b=-11}\\{a+b=-5}\end{array}\right.$的解,过点A作x轴的平行线d
如图,在平面直角坐标系中,点O为坐标原点,A(0,a),B(b,0),a与b为方程组$\left\{\begin{array}{l}{4a+3b=-11}\\{a+b=-5}\end{array}\right.$的解,过点A作x轴的平行线d查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $a≤\frac{1}{3}$ | B. | $a≥\frac{1}{3}$ | C. | $a>\frac{1}{3}$ | D. | $a<\frac{1}{3}$且a≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
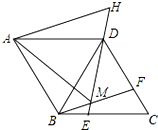 如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
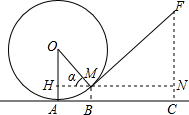 如图,圆形铁环向前滚动时,铁环钩MF保持与铁环相切,已知铁环的半径为20厘米,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=$\frac{3}{5}$.
如图,圆形铁环向前滚动时,铁环钩MF保持与铁环相切,已知铁环的半径为20厘米,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
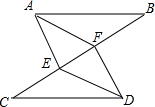 如图,E,F在线段BC上,AB=DC,AE=DF,BF=CE,下列结论不一定成立的是( )
如图,E,F在线段BC上,AB=DC,AE=DF,BF=CE,下列结论不一定成立的是( )| A. | ∠B=∠C | B. | AF=FD | C. | AE=DF | D. | AB∥DC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com