练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，六边形ABCDEF∽六边形GHIJKL，相似比为2：1，则下列结论正确的是（ ）

    A. ∠E=2∠K B. BC=2HI C. 六边形ABCDEF的周长=六边形GHIJKL的周长 D. S六边形ABCDEF=2S六边形GHIJKL

    【答案】B

    【解析】

    试题根据相似多边形的性质对各选项进行逐一分析即可．

    解：A、∵六边形ABCDEF∽六边形GHIJKL，∴∠E=∠K，故本选项错误；

    B、∵六边形ABCDEF∽六边形GHIJKL，相似比为2：1，∴BC=2HI，故本选项正确；

    C、∵六边形ABCDEF∽六边形GHIJKL，相似比为2：1，∴六边形ABCDEF的周长=六边形GHIJKL的周长×2，故本选项错误；

    D、∵六边形ABCDEF∽六边形GHIJKL，相似比为2：1，∴S六边形ABCDEF=4S六边形GHIJKL，故本选项错误．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，正方形网格中小方格边长为1，请你根据所学的知识解决下面问题．

    （1）求网格图中△ABC的面积．

    （2）判断△ABC是什么形状？并所明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边△ABD与等边△ACE，连接BE、CD，BE的延长线与CD交于点F，下列结论：（1）BE=CD ；（2）AF平分∠EAC ； （3）∠BFD=60°；（4）AF+FD=BF 其中正确的有（ ）

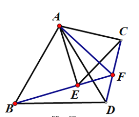
    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市创建“绿色发展模范城市”，针对境内长江段两种主要污染源：生活污水和沿江工厂污染物排放，分别用“生活污水集中处理”（下称甲方案）和“沿江工厂转型升级”（下称乙方案）进行治理，若江水污染指数记为Q，沿江工厂用乙方案进行一次性治理（当年完工），从当年开始，所治理的每家工厂一年降低的Q值都以平均值n计算．第一年有40家工厂用乙方案治理，共使Q值降低了12．经过三年治理，境内长江水质明显改善．

    （1）求n的值；

    （2）从第二年起，每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m，三年来用乙方案治理的工厂数量共190家，求m的值，并计算第二年用乙方案新治理的工厂数量；

    （3）该市生活污水用甲方案治理，从第二年起，每年因此降低的Q值比上一年都增加个相同的数值a．在（2）的情况下，第二年，用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等，第三年，用甲方案使Q值降低了39.5．求第一年用甲方案治理降低的Q值及a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．

    △ACB和△DCE的顶点都在格点上，ED的延长线交AB于点F．

    （1）求证：△ACB∽△DCE；（2）求证：EF⊥AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．

    下面有三个推断：

    ①当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；

    ②随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；

    ③若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的概率一定是0.620．

    其中合理的是（ ）

    A. ① B. ② C. ①② D. ①③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在 Rt△ABC 中，∠C=Rt∠，AC=2BC,AB=5,D、E 分别在 AB、AC 上，且 AE ,DE∥BC.

    （1）如图（1），将△ADE 沿射线 DA 方向平移，得到△ A1 D1 E1 ,当 AD1 多大时，四边形 AA1 E1 E 为菱形；

    （2）如图（2），将△ADE 绕 A 点顺时针旋转 度（ 00 1800 ）得到△AD2E2

    ①连结 CE2 , BD2 ,求：的值；

    ②连结 CE2 , BE2 若△ ACE2 是直角三角形，求：△ ABE 2 的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是 （ ）

    A. AB＝AC B. BD＝CD C. ∠B＝∠C D. ∠BDA＝∠CDA

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，PA，PB是⊙O的切线，A，B是切点，点C是劣弧AB上的一点，若∠P＝40°，则∠ACB等于(　　)

    A. 80° B. 110° C. 120° D. 140°

    查看答案和解析>>

    同步练习册答案