【题目】如图，EF∥AD，∠1=∠2．证明：∠DGA+∠BAC=180°．请完成说明过程．
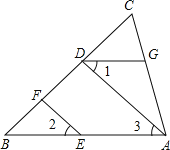
解：∵EF∥AD，（已知）
∴∠2=∠3．（ ）
又∵∠1=∠2（已知）
∴∠1=∠3，（等量代换）
∴AB∥ ，（ ）
∴∠DGA+∠BAC=180°．（ ）
科目：初中数学 来源： 题型：
【题目】如图，正方形
中，
，点
在
边上，点
在
边上，连接
、
、
，下列说法：①若为中点，
，则
；②若为中点，，则；③若，，则点为中点，正确的有（ ）个
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，AD∥BC，DE平分∠ADB，∠BDC＝∠BCD．
（1）求证：∠1+∠2＝90°；
（2）若∠ABD的平分线与CD的延长线交于F，且∠F＝55°，求∠ABC；
（3）若H是BC上一动点，F是BA延长线上一点，FH交BD于M，FG平分∠BFH，交DE于N，交BC于G．当H在BC上运动时（不与B点重合），试判断∠BAD+∠DMH与∠DNG的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在3×3的方格中，点A、B、C、D、E、F都是格点，从A、D、E、F四点中任意取一点，以所取点及B、C为顶点画三角形，所画三角形是直角三角形的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（问题背景）
（1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D；
（简单应用）
（2）如图2， AP、CP分别平分∠BAD． ∠BCD，若∠ABC=46°，∠ADC=26°，求∠P的度数；
（问题探究）
（3）如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，请猜想∠P的度数，并说明理由．
（拓展延伸）
（4） ①在图4中，若设∠C=α，∠B=β，∠CAP=
∠CAB，∠CDP=∠CDB，试问∠P与∠C、∠B之间的数量关系为： （用α、β表示∠P）；
②在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE， 猜想∠P与∠B、∠D的关系，直接写出结论．
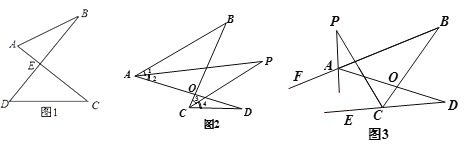
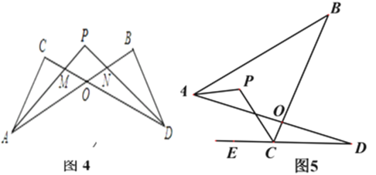
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C．
（1）试判断线段AB与AC的数量关系，并说明理由；
（2）若 
，求⊙O的半径和线段PB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知三角形ABC在平面直角坐标系中的位置如图所示．将三角形ABC向右平移6个单位长度，再向下平移6个单位长度得到三角形A1B1C1．(图中每个小方格边长均为1个单位长度) ．
（1）在图中画出平移后的三角形A1B1C1；
（2）求三角形ABC的面积；
（3）直接写出三角形A1B1C1各顶点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图二次函数 
的图象经过A（－1，0）和B（3，0）两点，且交 
轴于点C．
（1）试确定 
、 
的值；
（2）若点M为此抛物线的顶点，求△MBC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读小强同学数学作业本上的截图内容并完成任务：
解方程组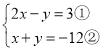
解：由①，得
，③ 第一步
把③代入①，得
．第二步
整理得，
．第三步
因为
可以取任意实数，所以原方程组有无数个解 第四步
任务：（1）这种解方程组的方法称为 ；
（2）利用此方法解方程组的过程中所体现的数学思想是 ；（请你填写正确选项）
A．转化思想 B．函数思想 C．数形结合思想 D．公理化思想
（3）小强的解法正确吗？ (填正确或不正确)，如果不正确，请指出错在第 步，请选择恰当的解方程组的方法解该方程组．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
