练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．若正多边形的一个内角等于120°，则这个正多边形的边数是6．

    分析 多边形的内角和可以表示成（n-2）•180°，因为所给多边形的每个内角均相等，故又可表示成120°n，列方程可求解．此题还可以由已知条件，求出这个多边形的外角，再利用多边形的外角和定理求解．

    解答 解：解法一：设所求正n边形边数为n，
    则120°n=（n-2）•180°，
    解得n=6；
    解法二：设所求正n边形边数为n，
    ∵正n边形的每个内角都等于120°，
    ∴正n边形的每个外角都等于180°-120°=60°．
    又因为多边形的外角和为360°，
    即60°•n=360°，
    ∴n=6．
    故答案为：6．

    点评 本题考查根据多边形的内角和计算公式求多边形的边数，解答时要会根据公式进行正确运算、变形和数据处理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

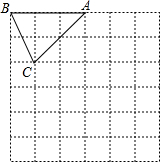    10．如图所示，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点A、B、C在小正方形的顶点上．将△ABC向下平移2个单位得到△A1B1C1，然后将△A1B1C1绕点C1顺时针旋转90°得到△A2B2C1．
    （1）在网格中画出△A1B1C1和△A2B2C1；
    （2）计算线段AC在变换到A2C1的过程中扫过区域的面积（重叠部分不重复计算）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

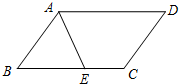    11．如图，在?ABCD中，AD=5，AB=3，AE平分∠BAD交BC边于点E．则线段BE、EC的长度分别为（　　）
    A．2和3B．3和2C．4和1D．1和4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，?ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，?ABCD满足矩形条件时，能判断四边形CODE是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算
    （1）（3.14-π）0-32+|-4|+（$\frac{1}{3}$）-2           
    （2）（-2a2b3）4+（-a）8•（2b4）3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

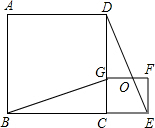    5．如图，四边形ABCD、CEFG都是正方形，点G在线段CD上，连接BG、DE，DE和FG相交于点O．设AB=a，CG=b（a＞b）．下列4个结论：
    ①△BCG≌△DCE；②BG⊥DE；③$\frac{DG}{GC}=\frac{GO}{CE}$；④$\frac{{S}_{△DGO}}{{S}_{△EOF}}=\frac{（a-b）^{2}}{{b}^{2}}$；其中结论正确的是①②④（填正确的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

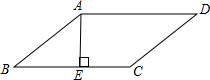    12．如图，在?ABCD中，AE⊥BC于E，AE=EB=EC=a，且a是一元二次方程x2+2x-3=0的根，则?ABCD的周长为（　　）
    A．4+2$\sqrt{2}$B．12+6$\sqrt{2}$C．2+2$\sqrt{2}$D．2+$\sqrt{2}$或12+6$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，已知在平行四边形ABCD中，对角线AC与BD交于点O，且BD⊥CD，若AD=13，CD=5，则BO的长度为6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图所示的平面纸能围成正方体盒子，请把与面A垂直的面用图中字母表示出来是B、C、E、F．

    查看答案和解析>>

    同步练习册答案