
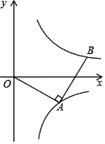
【题目】如图,OA=AB,∠OAB=90°,双曲线y=![]() 经过点A,双曲线y=﹣
经过点A,双曲线y=﹣![]() 经过点B,已知点A的纵坐标为﹣2,则点B的坐标为_____.
经过点B,已知点A的纵坐标为﹣2,则点B的坐标为_____.
【答案】![]()
【解析】
作AC⊥y轴于C,BD⊥AC于D,如图,设A(-![]() ,-2),则AC=-
,-2),则AC=-![]() ,OC=2,证明△AOC≌△BAD得到BD=AC=-
,OC=2,证明△AOC≌△BAD得到BD=AC=-![]() ,AD=OC=2,则B(-
,AD=OC=2,则B(-![]() +2,-
+2,-![]() -2),然后把B(-
-2),然后把B(-![]() +2,-
+2,-![]() -2)代入y=-
-2)代入y=-![]() 得(-
得(-![]() +2)(-
+2)(-![]() -2)=-k,然后解关于k的方程即可得到B点坐标.
-2)=-k,然后解关于k的方程即可得到B点坐标.
作AC⊥y轴于C,BD⊥AC于D,如图,

设A(-![]() ,-2),则AC=-
,-2),则AC=-![]() ,OC=2,
,OC=2,
∵∠OAB=90°,∠OCA=90°,
∴∠OAC+∠BAD=90°,∠OAC+∠AOC=90°,
∴∠AOC=∠BAD,
在△AOC和△BAD中,
 ,
,
∴△AOC≌△BAD(AAS),
∴BD=AC=-![]() ,AD=OC=2,
,AD=OC=2,
∴B(-![]() +2,-
+2,-![]() -2),
-2),
把B(-![]() +2,-
+2,-![]() -2)代入y=-
-2)代入y=-![]() 得(-
得(-![]() +2)(-
+2)(-![]() -2)=-k,
-2)=-k,
整理得k2+4k-16=0,解得k1=2![]() -2(舍去),k2=-2
-2(舍去),k2=-2![]() -2,
-2,
∴B点坐标为(3+![]() ,
,![]() -1).
-1).
故答案为(3+![]() ,
,![]() -1).
-1).


科目:初中数学 来源: 题型:
【题目】根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图,由图可知,下列说法错误的是( )

A.扇形统计图能反映各部分在总体中所占的百分比
B.每天阅读30分钟以上的居民家庭孩子超过50%
C.每天阅读1小时以上的居民家庭孩子占20%
D.每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是108°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各数填入相应的集合内:
![]() ,1.010010001,
,1.010010001,![]() ,22,-8,
,22,-8,![]() ,-1.232232223…,-1.414,0.
,-1.232232223…,-1.414,0.
正数集合{ ……}
负数集合{ ……}
有理数集合{ ……}
无理数集合{ ……}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x-4的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为d1,d2。
(1)求点A,B的坐标;
(2)当P为线段AB的中点时,求d1+d2的值;
(3)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;
(4)若在线段AB上存在无数个点P,使d1+ad2=4(a为常数),求a的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
查看答案和解析>>
科目:初中数学 来源: 题型:
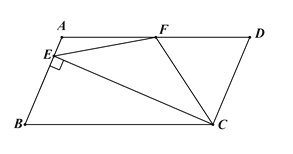
【题目】如图,在平行四边形 ABCD 中, AD 2 AB ;CF 平分 BCD 交 AD 于 F ,作 CE AB , 垂足 E 在边 AB 上,连接 EF .则下列结论:① F 是 AD 的中点; ② S△EBC 2S△CEF;③ EF CF ; ④ DFE 3AEF .其中一定成立的是_____.(把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
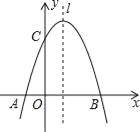
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月25日是全国中小学生安全教育日,某中学为加强学生的安全意识,组织了全校800名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.


(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n=
(2)补全频数分布直方图.
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
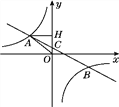
【题目】【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,-2).
,点B的坐标为(m,-2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com