
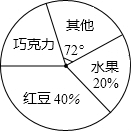
 如图是某冷饮店一天售出各种口味雪糕量的扇形统计图,其中售出红豆口味的雪糕160支,那么巧克力口味雪糕售出的数量是80支.
如图是某冷饮店一天售出各种口味雪糕量的扇形统计图,其中售出红豆口味的雪糕160支,那么巧克力口味雪糕售出的数量是80支.  寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
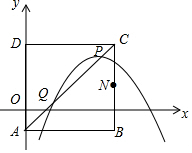 在平面直角坐标系中,己知正方形ABCD的顶点A的坐标为(0,-1),点B的坐标为(4,-1),顶点C在第一象限内,抛物线y=-$\frac{1}{2}$x2+bx+c(b、c常数)的顶点P为正方形对角线AC上一动点.
在平面直角坐标系中,己知正方形ABCD的顶点A的坐标为(0,-1),点B的坐标为(4,-1),顶点C在第一象限内,抛物线y=-$\frac{1}{2}$x2+bx+c(b、c常数)的顶点P为正方形对角线AC上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
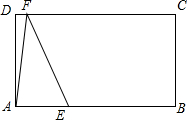 如图,在矩形ABCD中,AB=6,AD=2$\sqrt{3}$,E是AB边上一点,AE=2,F是直线CD上一动点,将△AEF沿直线EF折叠,点A的对应点为点A′,当点E,A′,C三点在一条直线上时,DF的长为6-2$\sqrt{7}$.
如图,在矩形ABCD中,AB=6,AD=2$\sqrt{3}$,E是AB边上一点,AE=2,F是直线CD上一动点,将△AEF沿直线EF折叠,点A的对应点为点A′,当点E,A′,C三点在一条直线上时,DF的长为6-2$\sqrt{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com