
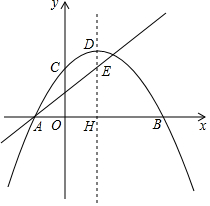
 ŅŃÖŖ£ŗČēĶ¼£¬Å×ĪļĻßy=-$\frac{1}{4}$£Øx-h£©2+kÓėxÖį½»ÓŚA”¢B£¬ÓėyÖį½»ÓŚC£¬Å×ĪļĻߵĶ„µćĪŖD£¬¶Ō³ĘÖį½»xÖįÓŚH£¬Ö±Ļßy=$\frac{3}{4}$x+$\frac{3}{2}$¾¹żµćAÓė¶Ō³ĘÖį½»ÓŚE£¬µćEµÄׯ×ų±źĪŖ3£®
ŅŃÖŖ£ŗČēĶ¼£¬Å×ĪļĻßy=-$\frac{1}{4}$£Øx-h£©2+kÓėxÖį½»ÓŚA”¢B£¬ÓėyÖį½»ÓŚC£¬Å×ĪļĻߵĶ„µćĪŖD£¬¶Ō³ĘÖį½»xÖįÓŚH£¬Ö±Ļßy=$\frac{3}{4}$x+$\frac{3}{2}$¾¹żµćAÓė¶Ō³ĘÖį½»ÓŚE£¬µćEµÄׯ×ų±źĪŖ3£®·ÖĪö £Ø1£©øł¾ŻŅŃÖŖĢõ¼žµĆµ½DµćµÄŗį×ų±źŹĒ2£¬ĒóµĆh=2°ŃA£Ø-2£¬0£©“śČėy=-$\frac{1}{4}$£Øx-h£©2+kµĆ£¬¼“æɵƵ½½įĀŪ£»
£Ø2£©ÉčPµÄŗį×ų±źĪŖt£¬Ōņׯ×ų±źĪŖ-$\frac{1}{4}$t2+t+3£¬øł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½ĮŠ·½³Ģ¼“æɵƵ½½įĀŪ£»
£Ø3£©ČēĶ¼2£¬¹żP×÷xÖį”¢yÖįµÄĘ½ŠŠĻß·Ö±š½»DH£¬KQÓŚM£¬N£¬½»Ö±ĻßDKÓŚR£¬ŌņĖıߊĪDKNM£¬ĖıߊĪKNPRŹĒ¾ŲŠĪ£¬ÉčMN=m£¬µĆµ½DK=KR=m£¬ĒóµĆPµćµÄŗį×ų±źĪŖ2m+2£¬“śČėy=-$\frac{1}{4}$£Øx-2£©2+4ÖŠµĆµ½PµćµÄׯ×ų±źĪŖ-m2+4øł¾ŻČż½ĒŗÆŹżµÄ¶ØŅåĮŠ·½³Ģ¼“æɵƵ½½įĀŪ£®
½ā“š 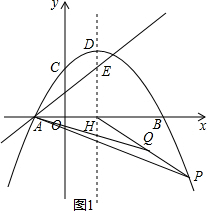 ½ā£ŗ£Ø1£©”ßµćEµÄׯ×ų±źĪŖ3£¬
½ā£ŗ£Ø1£©”ßµćEµÄׯ×ų±źĪŖ3£¬
”ą3=$\frac{3}{4}$x+$\frac{3}{2}$£¬
½āµĆ£ŗx=2£¬
”ąDµćµÄŗį×ų±źŹĒ2£¬
”ąh=2£¬
”ßÖ±Ļßy=$\frac{3}{4}$x+$\frac{3}{2}$¾¹żµćA£¬
”ąA£Ø-2£¬0£©“śČėy=-$\frac{1}{4}$£Øx-h£©2+kµĆ£¬0=-$\frac{1}{4}$£Ø-2-h£©2+k£¬
”ąk=4£»
£Ø2£©ČēĶ¼1£¬ÉčPµÄŗį×ų±źĪŖt£¬Ōņׯ×ų±źĪŖ-$\frac{1}{4}$t2+t+3£¬
”ßµćQĪŖPHµÄÖŠµć£¬
”ąS”÷APQ=S”÷AQH£¬
”ąS”÷APQ=$\frac{1}{2}$S”÷AHP£¬
”ßS”÷AHP=$\frac{1}{2}$AH£Ø$\frac{1}{4}$t2-t-3£©£¬
”ßAH=4£¬
”ąS=$\frac{1}{2}”Į\frac{1}{2}$”Į4”Į£Ø£Ø$\frac{1}{4}$t2-t-3£©=$\frac{1}{4}$t2-t-3£Øt£¾6£©£»
£Ø3£©ČēĶ¼2£¬¹żP×÷xÖį”¢yÖįµÄĘ½ŠŠĻß·Ö±š½»DH£¬KQÓŚM£¬N£¬½»Ö±ĻßDKÓŚR£¬
ŌņĖıߊĪDKNM£¬ĖıߊĪKNPRŹĒ¾ŲŠĪ£¬
ÉčMN=m£¬
”ąDK=KR=m£¬
”ąPµćµÄŗį×ų±źĪŖ2m+2£¬“śČėy=-$\frac{1}{4}$£Øx-2£©2+4ÖŠ£¬
µĆµ½PµćµÄׯ×ų±źĪŖ£ŗ-m2+4£¬”ąDM=RP=m2£¬
”ątan”ĻDKE=$\frac{m}{{m}^{2}}$=$\frac{1}{m}$£¬
”ą”ĻDKE=”ĻKPR£¬
”ąEK”ĶPK£¬
”ß2”ĻDKE+”ĻHPK=90”ć£¬”ĻDKE=”ĻKPR£¬”ĻBHP+”ĻHPK+”ĻKPR=90”ć£¬
”ą”ĻDKE=”ĻPHB£¬
”ątan”ĻDKE=tan”ĻPHB£¬
”ą$\frac{1}{m}$=$\frac{{m}^{2}-4}{2m}$£¬
”ąm=”Ą$\sqrt{6}$£Øm=-$\sqrt{6}$ÉįČ„£©£¬
”ąm=$\sqrt{6}$£¬
”ąµćPµÄŗį×ų±źĪŖ2+2$\sqrt{6}$£®
µćĘĄ ±¾Ģāæ¼²éĮĖŅ»“ĪŗÆŹżŗĶ¶ž“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷£¬Čż½ĒŠĪĆ껿µÄ¼ĘĖć£¬¾ŲŠĪµÄŠŌÖŹ£¬½āÖ±½ĒČż½ĒŠĪ£¬ÕżČ·µÄ×÷³öøØÖśĻߏĒ½āĢāµÄ¹Ų¼ü£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | Ę½¾łŹż | B£® | ÖŠĪ»Źż | C£® | ÖŚŹż | D£® | ·½²ī |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 0.11”Į108 | B£® | 1.1”Į109 | C£® | 1.1”Į1010 | D£® | 11”Į108 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
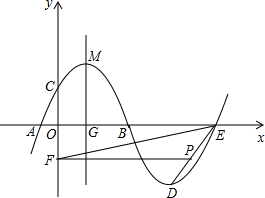 ČēĶ¼£¬Å×ĪļĻßm£ŗy=-0.25£Øx+h£©2+kÓėxÖįµÄ½»µćĪŖA£¬B£¬ÓėyÖįµÄ½»µćĪŖC£¬¶„µćĪŖM£Ø3£¬6.25£©£¬½«Å×ĪļĻßmČʵćBŠż×Ŗ180”ć£¬µĆµ½ŠĀµÄÅ×ĪļĻßn£¬ĖüµÄ¶„µćĪŖD£®
ČēĶ¼£¬Å×ĪļĻßm£ŗy=-0.25£Øx+h£©2+kÓėxÖįµÄ½»µćĪŖA£¬B£¬ÓėyÖįµÄ½»µćĪŖC£¬¶„µćĪŖM£Ø3£¬6.25£©£¬½«Å×ĪļĻßmČʵćBŠż×Ŗ180”ć£¬µĆµ½ŠĀµÄÅ×ĪļĻßn£¬ĖüµÄ¶„µćĪŖD£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
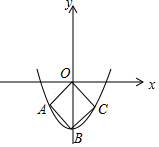 ČēĶ¼£¬Å×ĪļĻßy=$\frac{1}{2}$x2+cµÄ¶„µćBŌŚyÖįµÄøŗ°ėÖįÉĻ£¬Õż·½ŠĪOABCµÄĮ½øö¶„µćA£¬CŌŚÅ×ĪļĻßÉĻ£¬ŌņcµÄÖµŹĒ-4£®
ČēĶ¼£¬Å×ĪļĻßy=$\frac{1}{2}$x2+cµÄ¶„µćBŌŚyÖįµÄøŗ°ėÖįÉĻ£¬Õż·½ŠĪOABCµÄĮ½øö¶„µćA£¬CŌŚÅ×ĪļĻßÉĻ£¬ŌņcµÄÖµŹĒ-4£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | µŚŅ»”¢ČżĻóĻŽ | B£® | µŚŅ»”¢¶žĻóĻŽ | C£® | µŚ¶ž”¢ĖÄĻóĻŽ | D£® | µŚ¶ž”¢ČżĻóĻŽ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
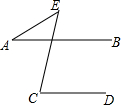 ČēĶ¼ĖłŹ¾£¬ŅŃÖŖAB”ĪCD£¬”ĻC=75”ć£¬”ĻA=25”ć£¬Ēó”ĻEµÄ¶ČŹż£®
ČēĶ¼ĖłŹ¾£¬ŅŃÖŖAB”ĪCD£¬”ĻC=75”ć£¬”ĻA=25”ć£¬Ēó”ĻEµÄ¶ČŹż£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com