(1)证明:∵锐角△ABC中,A关于BC的对称点为D,B关于AC为E.
∴CD=CA,CE=CB,∠CMD=∠CNE=90°,∠DCM=∠ACM,∠ECN=∠BCN,
∴∠DCM=∠ECN,
∵CB=CA,
∴CD=CE,
在△CDM和△CEN中,
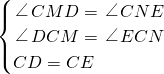
,
∴△CDM≌△CEN(AAS);
(2)解:当锐角△ABC是等腰三角形且顶角∠ACB=45°时,四边形CDFE为菱形.
若四边形CDFE为菱形,则需CD=CE,CD∥EF,
∴由(1)得:当△ABC为等腰三角形,即CB=CA时,△CDM≌△CNE,此时CD=CE,
∴∠CDM=∠CEN,
设∠DCM=∠ECN=∠ACB=x°,
∵∠CNE=90°,
∴∠CEN=90°-x°,
∵CD∥EF,
∴∠DCE+∠CEN=180°,
∴3x+90-x=180,
解得:x=45,
∴∠ACB=45°,
即当锐角△ABC是等腰三角形且顶角∠ACB=45°时,四边形CDFE为菱形.
(3)解:当∠ACB=60°时,点C在DE直线上;当0°<∠ACB<60°或60°<∠ACB<90°时,C在直线DE外.
理由:∵若点C在DE直线上,则需D,C,E三点共线,
即∠DCE=180°,
∵∠DCM=∠ACB=∠ECN,
∴∠ACB=60°,
∴当∠ACB=60°时,点C在DE直线上;
∵△ACB是锐角三角形,
∴当0°<∠ACB<60°或60°<∠ACB<90°时,C在直线DE外.
综上可得:当∠ACB=60°时,点C在DE直线上;当0°<∠ACB<60°或60°<∠ACB<90°时,C在直线DE外.
分析:(1)由锐角△ABC中,A关于BC的对称点为D,B关于AC为E,△ABC为等腰三角形,即CB=CA.易证得CD=CA=CE=CB,∠DCM=∠ACB=∠ECN,∠CMD=∠CNE=90°,则可由AAS判定:△CDM≌△CEN;
(2)由若四边形CDFE为菱形,则需CD=CE,CD∥EF,由(1)可得当△ABC为等腰三角形,即CB=CA时,△CDM≌△CNE,此时CD=CE,然后设∠DCM=∠ECN=∠ACB=x°,易求得∠ACB=45°,即可得当锐角△ABC是等腰三角形且顶角∠ACB=45°时,四边形CDFE为菱形;
(3)由若点C在DE直线上,则需D,C,E三点共线,即∠DCE=180°,可求得当∠ACB=60°时,点C在DE直线上;又由△ACB是锐角三角形,可得当0°<∠ACB<60°或60°<∠ACB<90°时,C在直线DE外.
点评:此题考查了菱形的判定与性质、全等三角形的判定与性质以及轴对称的性质.此题难度较大,注意掌握数形结合思想与方程思想的应用.

 如图,锐角△ABC中,A关于BC的对称点为D,B关于AC为E.
如图,锐角△ABC中,A关于BC的对称点为D,B关于AC为E.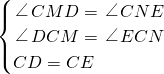 ,
,

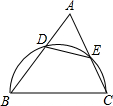 (1997•浙江)如图,锐角△ABC中,以BC为直径的半圆分别交AB,AC于点D,E,记△ADE的面积为S1,△ABC的面积为S2,则
(1997•浙江)如图,锐角△ABC中,以BC为直径的半圆分别交AB,AC于点D,E,记△ADE的面积为S1,△ABC的面积为S2,则