练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知（a+2）2+|b-$\frac{1}{4}$|=0，求5a2b-[2a2b-（ab2-2a2b）-4]-2ab2的值．

    分析 原式去括号合并得到最简结果，利用非负数的性质求出x与y的值，代入计算即可求出值．

    解答 解：原式=5a2b-2a2b+ab2-2a2b+4-2ab2=a2b-ab2+4，
    ∵（a+2）2+|b-$\frac{1}{4}$|=0，
    ∴a=-2，b=$\frac{1}{4}$，
    则原式=5$\frac{1}{8}$．

    点评 此题考查了整式的加减-化简求值，以及非负数的性质，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．如图，一次函数y=-x+3的图象与x，y轴分别交于点A，B，点C、点B关于点M（0，2）对称．
    （1）求C点坐标；
    （2）设过B、C两点的圆的圆心为P
    ①若P点横坐标为-3，圆P交x轴于点E、F（E在F的左侧），分别求sin∠BEC和sin∠BFC的值；
    ②对于常数a（a＞1），x轴上是否存在点Q，使得sin∠BQC=$\frac{1}{a}$？若存在，求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．设圆O1，圆O2交于点A，B，过A作直线CD交圆O1，圆O2于C，D，M为CD的中点，P为O1O2的中点．求证：PM=PA．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

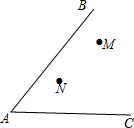    10．如图，南开中学高二年级的学生分别在五云山寨M，N两处参加社会时间活动．先要在道路AB，AC形成的锐角∠BAC内设一个休息区P，使P到两条道路的距离相等，并且使得PM=PN，请用直尺和圆规作出P点的位置（不写作法，值保留作图痕迹）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．在数轴上分别画出表示$\sqrt{8}$和$\sqrt{3}$的数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列各式中，一定能成立的是（　　）
    A．$\sqrt{{（-2）}^{2}}$=${（-\sqrt{2}）}^{2}$B．$\sqrt{{（\sqrt{7}-3）}^{2}}$=$\sqrt{7}$-3C．$\sqrt{{x}^{2}+2x+1}$=x+1D．$\sqrt{{x}^{2}-25}$=$\sqrt{x+5}$•$\sqrt{x-5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知关于x的方程x2+mx+m-2=0．
    （1）若该方程的两根x1，x2满足x1+x2-x1•x2=-2，求m的值；
    （2）求证：不论m取何实数，该方程都有两个不相等的实数根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．用两张大小及形状均相同的直角三角形纸片拼图，可拼成（　　）种不同的图形．
    A．4B．5C．6D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．已知平行四边形ABCD的两条对角线相交于直角坐标系的原点，点A，B的坐标分别为（-2，-3），（-1，2），则C、D的坐标分别为（2，3）（1，-2）．

    查看答案和解析>>

    同步练习册答案