
 如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )
如图,在梯形ABCD中,AD∥BC,AB=DC,BC-AD=AB,过D作DE∥AB交BC于E,则△DEC是( )| A. | 不等边三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
科目:初中数学 来源: 题型:解答题
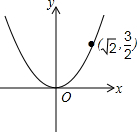 如图,已知二次函数y=ax2的图象经过点($\sqrt{2}$,$\frac{3}{2}$).
如图,已知二次函数y=ax2的图象经过点($\sqrt{2}$,$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
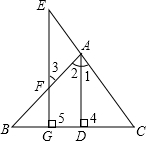 已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.
已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
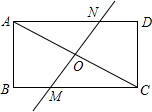 如图,将矩形ABCD沿直线MN对折,使A、C重合,直线MN交AC于O,且AB=6,BC=8
如图,将矩形ABCD沿直线MN对折,使A、C重合,直线MN交AC于O,且AB=6,BC=8查看答案和解析>>
科目:初中数学 来源: 题型:选择题
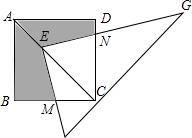 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )
如图,点E在正方形ABCD的对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为2,图中阴影部分的面积为( )| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{16}{9}$ | D. | $\frac{20}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,为了躲避海盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围25海里内有暗礁,若轮船仍向前航行,有无触礁的危险?你对船长有何建议?
如图所示,为了躲避海盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围25海里内有暗礁,若轮船仍向前航行,有无触礁的危险?你对船长有何建议?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com