
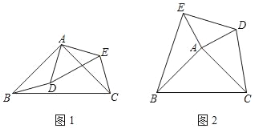
【题目】已知,等腰△ABC和等腰△ADE中,∠BAC=∠DAE=90°.
(1)如图1,求证:DB=CE;
(2)如图2.求证:S△ACD=S△ABE.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据SAS证明△BAD≌△CAE即可解决问题;
(2)如图2中,取CD的中点M,连接AM,延长AM到N,使得MN=AM,连接DN,CN.首先证明四边形ACND是平行四边形,再证明△BAE≌△ACN即可.
(1)证明:如图1中,
∵等腰△ABC和等腰△ADE中,∠BAC=∠DAE=90°,
∴AB=AC,AD=AD,∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE.
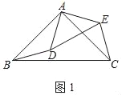
(2)证明:如图2中,取CD的中点M,连接AM,延长AM到N,使得MN=AM,连接DN,CN.
∵AM=MN,DM=CM,
∴四边形ACND是平行四边形,
∴AD=CN,AD∥CN,
∴∠DAC+∠ACN=180°,
∵∠BAC=∠EAD=90°,
∴∠BAE+∠DAC=180°,
∴∠BAE=∠ACN,
∵AB=AC,AE=AD=CN,
∴△BAE≌△ACN(SAS),
∴S△BAE=S△ACN,
∵DN∥AC,
∴S△ADC=S△ACN,
∴S△BAE=S△ADC.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
(1)写出点A的坐标.
(2)画出△OAB绕点O顺时针旋转90°后的△OA1B1;
(3)求点A旋转到点A1所经过的路线长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个变量![]() 之间的变化情况如图所示,根据图像回答下列问题.
之间的变化情况如图所示,根据图像回答下列问题.
(1)写出![]() 的变化范围;
的变化范围;
(2)当![]() 时,求
时,求![]() 的对应值;
的对应值;
(3)当![]() 为何值时,
为何值时,![]() 的值最大;
的值最大;
(4)当![]() 在什么范围时,
在什么范围时,![]() 的值在不断增加.
的值在不断增加.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校以下是他本次上学所用的时间与路程的关系示意图.

根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是________米
(2)小明在书店停留了___________分钟.
(3)本次上学途中,小明一共行驶了________ 米,一共用了______ 分钟.
(4)在整个上学的途中_________(哪个时间段)小明骑车速度最快,最快的速度是___________米/分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,A(2,2),B(4,﹣3),P是x轴上的一点.
(1)若PA+PB的值最小,求P点的坐标;
(2)若∠APO=∠BPO.
①求此时P点的坐标;
②在y轴上是否存在点Q,使得△QAB的面积等于△PAB的面积,若存在,求出Q点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B是数轴上的两个点,它们分别表示的数是![]() 和1. 点A与点B之间的距离表示为AB.
和1. 点A与点B之间的距离表示为AB.
(1)AB= .
(2)点P是数轴上A点右侧的一个动点,它表示的数是![]() ,满足
,满足![]() ,求
,求![]() 的值.
的值.
(3)点C为6. 若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.请问:![]() 的值是否随着运动时间t(秒)的变化而改变? 若变化,请说明理由;若不变,请求其值.
的值是否随着运动时间t(秒)的变化而改变? 若变化,请说明理由;若不变,请求其值.
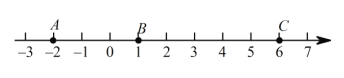
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,BC=8,∠BAC=120°,作AD⊥BC于点D,AD=![]() AB,点E为边AC上的中点,点P为BC上一动点,则PA+PE的最小值为_______.
AB,点E为边AC上的中点,点P为BC上一动点,则PA+PE的最小值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的等边△ABC中,D是BC的中点,点E在线段AD上,连结BE,在BE的下方作等边△BEF,连结DF.当△BDF的周长最小时,∠DBF的度数是_____.
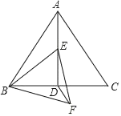
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com