
【题目】已知矩形ABCD中,AB=3,BC=4,E,F两点分别在边AB,BC上运动,△BEF沿EF折叠后为△GEF,
(1)若BF=a,则线段AG的最小值为 . (用含a的代数式表示)
(2)问:在E、F运动过程中,取a= 时,AG有最小值,值为 .
科目:初中数学 来源: 题型:
【题目】解不等式组 ![]() .请结合题意填空,完成本题的解答.
.请结合题意填空,完成本题的解答.
(1)解不等式①,得:;
(2)解不等式②,得:;
(3)把不等式①和②的解集在数轴上表示出来; ![]()
(4)不等式组的解集为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列每个图形及相应推出的结论,其中正确的是( )
A.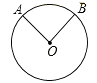
∵ ![]()
∴∠AOB=80°
B.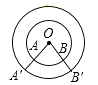
∵∠AOB=∠A′O′B′
∴ ![]()
C.
∵ ![]()
∴AB=CD
D.
∵MN垂直平分AD
∴ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形.
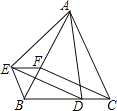
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1,可以得到![]() 这个等式,请解答下列问题:
这个等式,请解答下列问题:

(1)写出图2中所表示的数学等式______________;(最后结果)
(2)根据整式乘法的运算法则,通过计算验证上述等式;
(3)利用(1)中得到的结论,解决问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2的值;
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出一个面积为(5a+2b)(3a+5b)的长方形,求x+y+z的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校申报“跳绳特色运动”学校一年后,抽样调查了部分学生的“1分钟跳绳”成绩,并制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图. 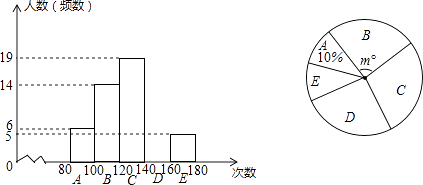
(1)补全频数分布直方图,扇形图中m=;
(2)若把每组中各个数据用这组数据的中间值代替(如A组80≤x<100的中间值是 ![]() =90次),则这次调查的样本平均数是多少?
=90次),则这次调查的样本平均数是多少?
(3)如果“1分钟跳绳”成绩大于或等于120次为优秀,那么该校2100名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心、OB为半径作圆,且⊙O过A点. 如图①,若⊙O的半径为5,求线段OC的长;
如图②,过点A作AD∥BC交⊙O于点D,连接BD,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,AD⊥AB,交BC于点D,AD=4,则BC的长为( )

A. 8 B. 4 C. 12 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传节约用水,小明随机调查了某小区部分家庭5月份的用水情况,并将收集的数据整理成如图所示的统计图.
(1)小明一共调查了多少户家庭?
(2)求所调查家庭5月份用水量的众数、平均数.
(3)若该小区有400户居民,请你估计这个小区5月份的用水量.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com