
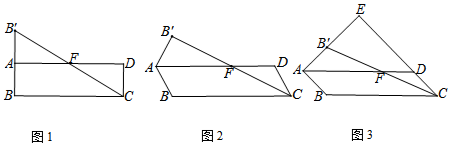
分析 (1)证明:根据已知条件得到□ABCD为矩形,AB=CD,根据矩形的性质得到∠D=∠BAD=90°,根据全等三角形的性质即可得到结论;
(2)方法1:如图2,过点B′作B′G∥CD交AD于点G,由轴对称的性质得到∠1=∠2,AB=AB′,根据平行线的性质得到∠2=∠3,∠1=∠3,根据平行线的性质得到∠4=∠D,根据全等三角形的性质即可得到结论;方法2:连接BB′交直线AD于H点,根据线段垂直平分线的性质得到B′H=HB,由平行线分线段成比例定理得到结论;方法3:连接BB′,BF,根据轴对称的性质得到AD是线段B′B的垂直平分线,根据线段垂直平分线的性质得到B′F=FB,得到∠1=∠2,由平行线的性质得到∠B′BC=90°,根据余角的性质得到∠3=∠4,于是得到结论;
(3)取B′E的中点G,连结GF,由(2)得,F为CB′的中点,根据平行线的性质得到∠BAD=180°-∠ABC=45°,由对称性的性质得到∠EAD=∠BAD=45°,根据平行线的性质得到∠GFA=∠FAB=45°,根据三角函数的定义即可得到结论.
解答 (1)证明:
∵四边形ABCD为平行四边形,∠ABC=90°,
∴□ABCD为矩形,AB=CD,
∴∠D=∠BAD=90°,
∵B,B′关于AD对称,
∴∠B′AD=∠BAD=90°,AB=AB′,
∴∠B′AD=∠D,
∵∠AFB′=∠CFD,
在△AFB′与△CFD中,$\left\{\begin{array}{l}{∠B′AD=∠D}\\{∠AFB′=∠CFD}\\{AB′=CD}\end{array}\right.$,
∴△AFB′≌△CFD(AAS),
∴FB′=FC,
∴F是CB′的中点;
(2)证明:
方法1:如图2,过点B′作B′G∥CD交AD于点G,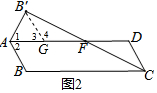
∵B,B′关于AD对称,
∴∠1=∠2,AB=AB′,
∵B′G∥CD,AB∥CD,
∴B′G∥AB.
∴∠2=∠3,
∴∠1=∠3,
∴B′A=B′G,
∵AB=CD,AB=AB′,
∴B′G=CD,
∵B′G∥CD,
∴∠4=∠D,
∵∠B′FG=∠CFD,
在△B′FG与△CFD中$\left\{\begin{array}{l}{∠4=∠D}\\{∠B′FG=∠DFC}\\{B′G=CD}\end{array}\right.$,
∴△B′FG≌△CFD(AAS),
∴FB′=FC,
∴F是CB′的中点;
方法2:连接BB′交直线AD于H点,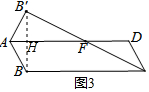
∵B,B′关于AD对称,
∴AD是线段B′B的垂直平分线,
∴B′H=HB,
∵AD∥BC,
∴$\frac{B′F}{FC}$=$\frac{B′H}{HB}$=1,
∴FB′=FC.
∴F是CB′的中点;
方法3:连接BB′,BF,
∵B,B′关于AD对称,
∴AD是线段B′B的垂直平分线,
∴B′F=FB,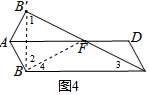
∴∠1=∠2,
∵AD∥BC,
∴B′B⊥BC,
∴∠B′BC=90°,
∴∠1+∠3=90°,∠2+∠4=90°,
∴∠3=∠4,
∴FB=FC,
∴B′F=FB=FC,
∴F是CB′的中点;
(3)解:取B′E的中点G,连结GF,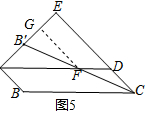
∵由(2)得,F为CB′的中点,
∴FG∥CE,FG=$\frac{1}{2}$CE,
∵∠ABC=135°,□ABCD中,AD∥BC,
∴∠BAD=180°-∠ABC=45°,
∴由对称性,∠EAD=∠BAD=45°,
∵FG∥CE,AB∥CD,
∴FG∥AB,
∴∠GFA=∠FAB=45°,
∴∠FGA=90°,GA=GF,
∴FG=sin∠EAD•AF=$\frac{\sqrt{2}}{2}$AF,
∴由①,②可得$\frac{CE}{AF}$=$\sqrt{2}$.
点评 本题考查了全等三角形的判定和性质,平行四边形的性质,平行线的性质,平行线分线段成比例定理,三角函数的定义,正确的作出辅助线是解题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-4mx+2m-1(m≠0)与平行于x轴的一条直线交于A,B两点.
在平面直角坐标系xOy中,抛物线y=mx2-4mx+2m-1(m≠0)与平行于x轴的一条直线交于A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
同时抛掷A,B两个均匀的小正方体(每个面上分别标有数字1、2、3、4、5、6),设两个正方体朝上的数字分别是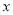 ,
,  ,并 以此确定点
,并 以此确定点 ,那么点P落在抛物线
,那么点P落在抛物线 上的概率是( )
上的概率是( )
A.  B.
B. 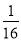 C.
C. 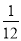 D.
D. 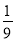
查看答案和解析>>
科目:初中数学 来源:2017届湖北省枝江市九年级3月调研考试数学试卷(解析版) 题型:单选题
下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )(单位:cm.)
A. 3,4,8 B. 8,7,15
C. 5,5,11 D. 13,12,20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com