
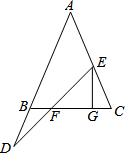
 如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系.
如图,∠ABC=∠C,点E在线段AC上,D在AB的延长线上,且有BD=CE,连接DE交BC于F,过E作FG⊥BC于G.试说明线段EF、FG、CG之间的数量关系. 分析 可在BC上截取GH=GC,可得△EHC是等腰三角形,进而得出AB∥EH,再证△BDF≌△HEF,通过线段之间的转化即可得出结论.
解答 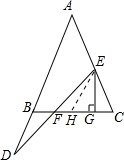 证明:在BC上截取GH=GC,连接EH,
证明:在BC上截取GH=GC,连接EH,
∵EG⊥BC,GH=GC,
∴EH=EC,
∴∠EHC=∠C,
又AB=AC,
∴∠ABC=∠C,
∴∠EHC=∠ABC,
∴EH∥AB,
∴∠DBF=∠EHF,∠D=∠DEH,
又EH=EC=BD,
∴△BDF≌△HEF,
∴BF=FH,
∴FG=FH+HG=BF+GC.
点评 本题主要考查了全等三角形的判定及性质问题、平行线的判定和性质、线段的垂直平分线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一条直线有且只有一条垂线 | |
| B. | 过一点有且只有一条直线与已知直线平行 | |
| C. | 不相等的两个角一定不是对顶角 | |
| D. | 相等的角不可能是邻补角 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ±(a+1) | B. | ±a+1 | C. | ±$\sqrt{{a}^{2}+1}$ | D. | ±$\sqrt{a+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
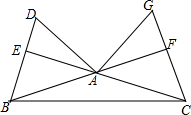 已知:如图:在钝角△ABC中,BE、CF分别是AC、AB两边上的高,在射线BE上截取BD=AC,在射线CF的延长线上截取CG=AB,连结AD、AG.
已知:如图:在钝角△ABC中,BE、CF分别是AC、AB两边上的高,在射线BE上截取BD=AC,在射线CF的延长线上截取CG=AB,连结AD、AG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
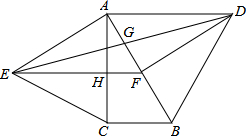 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;其中正确结论的为①③(请将所有正确的序号都填上).
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;其中正确结论的为①③(请将所有正确的序号都填上).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com