
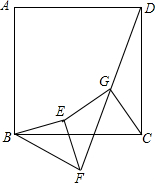
 已知正方形ABCD,△BEF是等腰直角三角形(BE=EF),联结FD,在FD上取中点G,联结EC和CG,求证:
已知正方形ABCD,△BEF是等腰直角三角形(BE=EF),联结FD,在FD上取中点G,联结EC和CG,求证:分析 (1)连接BD取BD中点O,取BF中点Q,连接OG、EQ、GQ、OC.只要证明△EQG≌△GOC即可.
(2)QG与OC交于点O′,先证明∠GO′C=90°,再利用全等三角形的性质即可解决问题.
解答 证明:(1)连接BD取BD中点O,取BF中点Q,连接OG、EQ、GQ、OC.
∵DO=OB,DG=GF,
∴OG=$\frac{1}{2}$BF,OG∥BF,
∵DG=GF,FQ=QF,
∴GQ∥BD,GQ=$\frac{1}{2}$BD,
∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°,
∴OC=$\frac{1}{2}$BD=QG,OC⊥BD,
∴∠GOC=90°-∠OGQ,
∵BE=EF,∠BEF=90°,
∴EQ⊥BF,∠EQF=90°,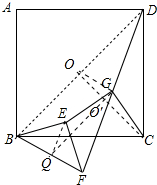
∴∠EQG=90°-∠GQF,
∵∠OGQ=∠GQF,
∴∠GOC=∠EQG,
在△EQG和△GOC中,
$\left\{\begin{array}{l}{EQ=OG}\\{∠EQG=∠GOC}\\{GQ=OC}\end{array}\right.$,
∴△EQG≌△GOC,
∴GC=EQ.
(2)QG与OC交于点O′.
∵△EQG≌△GOC,
∴∠EGQ=∠GCO,
∵OC⊥BD,QG∥BD,
∴OC⊥QG,∠GO′C=90°
∴∠OCG+∠QGC=90°,
∴∠EGQ+∠QGC=90°
∴∠EGC=90°,
∴EG⊥GC.
点评 本题考查全等三角形的判定和性质、正方形的性质、三角形中位线定理、等腰直角三角形的性质等知识,解题的关键是添加辅助线构造全等三角形,学会利用三角形中位线添加辅助线,掌握证明垂直的方法,属于中考常考题型.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:选择题
| A. | x≥$\frac{3}{4}$ | B. | x≤$\frac{3}{4}$ | C. | x<$\frac{3}{4}$ | D. | x≠$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
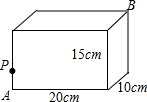 如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少?
如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
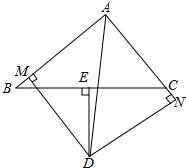 如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN.
如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
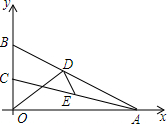 如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )
如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<0 | B. | x<$\frac{1}{2}$ | C. | x$≥\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k≠-3 | B. | k≠5 | C. | k≠-3且k≠-5 | D. | k≠-3且k≠5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
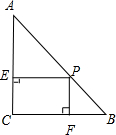 已知△ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,AB上有一动点P,过点P作PE⊥AC于E,PF⊥BC于F.
已知△ABC中,AC=BC=3$\sqrt{2}$,∠C=90°,AB上有一动点P,过点P作PE⊥AC于E,PF⊥BC于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com