
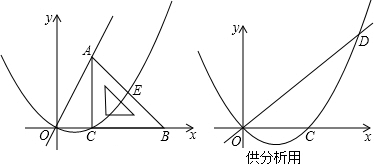
分析 (1)根据题意易得点A的横坐标与点C的相同,点A的纵坐标即是线段AC的长度;把点A的坐标代入直线OA的解析式来求k的值;
(2)①求得抛物线y1的顶点坐标,然后把该坐标代入函数y=-$\frac{1}{2}$x2,若该点满足函数解析式y=-$\frac{1}{2}$x2,即表示该顶点在函数y=-$\frac{1}{2}$x2图象上;反之,该顶点不在函数y=-$\frac{1}{2}$x2图象上;
②如图1,过点E作EK⊥x轴于点K.则EK是△ACB的中位线,所以根据三角形中位线定理易求点E的坐标,把点E的坐标代入抛物线y1=$\frac{1}{2}$x(x-m)即可求得m=1;
(3)如图2,根据抛物线与直线相交可以求得点D横坐标是$\frac{2}{am}$+m.则m+2=$\frac{2}{am}$+m,由此可以求得a与m的关系式.
解答 解:(1)∵等腰Rt△ABC的直角边 BC=2,
∵点 C 的横坐标为m,
∴AC=2,
∴点A的坐标是(m,2).
又∵直线OA:y2=kx(k为常数,k>0),
∴2=km,则k=$\frac{2}{m}$(k>0).
故答案为:m,2;$\frac{2}{m}$(k>0).
(2)①当a=$\frac{1}{2}$时,y1=$\frac{1}{2}$x(x-m),其顶点坐标为($\frac{m}{2}$,-$\frac{{m}^{2}}{8}$).
对于y=-$\frac{1}{2}$x2来说,当x=$\frac{m}{2}$时,y=-$\frac{1}{2}$×$\frac{{m}^{2}}{4}$=-$\frac{{m}^{2}}{8}$,即点($\frac{m}{2}$,-$\frac{{m}^{2}}{8}$)在抛物线y=-$\frac{1}{2}$x2上.
故当a=$\frac{1}{2}$时,抛物线y1=ax(x-m)的顶点在函数y=-$\frac{1}{2}$x2的图象上;
②如图,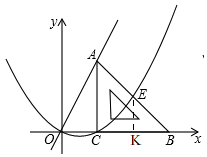
过点E作EK⊥x轴于点K.
∵AC⊥x轴,
∴AC∥EK.
∵点E是线段AB的中点,
∴K为BC的中点,
∴EK是△ACB的中位线,
∴EK=$\frac{1}{2}$AC=1,CK=$\frac{1}{2}$BC=1,
∴E(m+1,1).
∵点E在抛物线y1=$\frac{1}{2}$x(x-m)上,
∴$\frac{1}{2}$(m+1)(m+1-m)=1,
解得m=1.
(3)如图2,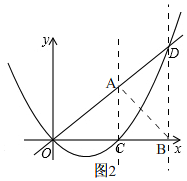
∵直线OA与抛物线的另一个交点为点D
∴$\left\{\begin{array}{l}{y=\frac{2}{m}x}\\{y=a(x-m)}\end{array}\right.$,则$\frac{2}{m}$x=ax(x-m),
解得x=$\frac{2}{am}+m$,或x=0(不合题意,舍去).
故点D的横坐标是$\frac{2}{am}+m$,
当x=$\frac{2}{am}+m$,时,|y2-y1|=0,由题意得m+2=$\frac{2}{am}+m$,
∴am=1.
∵y2-y1=$\frac{2}{m}$x-ax(x-m)=-ax2+(am+$\frac{2}{m}$)x=-a[x2-(m+$\frac{2}{am}$)x+($\frac{m}{2}$+$\frac{1}{am}$)2]+a($\frac{m}{2}$+$\frac{1}{am}$)2
=-a[x-($\frac{m}{2}$+$\frac{1}{am}$)]2+a($\frac{m}{2}$+$\frac{1}{am}$)2
∴当x=$\frac{m}{2}$+$\frac{1}{am}$时,y2-y1取得最大值,
又∵当x=$\frac{2}{am}+m$时,|y2-y1|=0,
∴当$\frac{m}{2}$+$\frac{1}{am}$≤x≤$\frac{2}{am}$+m时,|y2-y1|随x的增大而减小;当x≥$\frac{2}{am}$+m时,|y2-y1|随x的增大而增大.
根据题意需要满足当m≤x≤m+2,|y2-y1|的值随x的增大而减小,当x≥m+2时,|y2-y1|的值随x的增大而增大,
∴m≥$\frac{m}{2}$+$\frac{1}{am}$可满足条件,
∵am=1,
∴解得m≥2.
综上所述,a与m的关系式及m的取值范围为am=1(m≥2).
点评 此题是二次函数综合题,主要考查了坐标与图形的性质、二次函数图象上点的坐标特征、一次函数与二次函数交点坐标等知识点.解题时,注意“数形结合”数学思想的应用.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:解答题
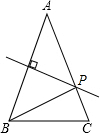 如图,△ABC中,AB=AC,AB的垂直平分线交AC于P点.
如图,△ABC中,AB=AC,AB的垂直平分线交AC于P点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 以上均可以 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+b | B. | abc | C. | 1000a+10b+c | D. | 100c+10b+a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
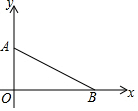 如图,点A的坐标为(0,1),点B的坐标为(2,0),若△ABC是等腰三角形,且点C在坐标轴上,则满足条件的点C有( )
如图,点A的坐标为(0,1),点B的坐标为(2,0),若△ABC是等腰三角形,且点C在坐标轴上,则满足条件的点C有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com