练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

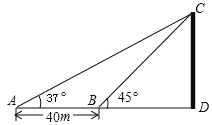
    【题目】如图，小明在地面A处利用测角仪观测气球C的仰角为37°，然后他沿正对气球方向前进了40m到达地面B处，此时观测气球的仰角为45°．求气球的高度是多少？参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75

    【答案】120m

    【解析】

    在Rt△ACD和Rt△BCD中，设CD＝x，分别用x表示AD和BD的长度，然后根据已知AB＝40m，列出方程求出x的值，继而可求得气球离地面的高度．

    设CD＝x，

    在Rt△BCD中，

    ∵∠CBD＝45°，

    ∴BD＝CD＝x，

    在Rt△ACD中，

    ∵∠A＝37°，

    ∴tan37°＝，

    ∴AD＝，

    ∵AB＝40m，

    ∴AD﹣BD＝﹣x＝40，

    解得：x＝120，

    ∴气球离地面的高度约为120（m）．

    答：气球离地面的高度约为120m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，弦DE垂直半径OA，C为垂足，DE＝6，连接DB，，过点E作EM∥BD，交BA的延长线于点M．

    （1）求的半径；

    （2）求证：EM是⊙O的切线；

    （3）若弦DF与直径AB相交于点P，当∠APD＝45°时，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，点是中点.连接.作，垂足为，的外接圆交于点，连接.

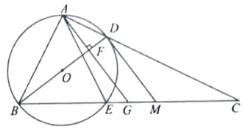
    （1）求证：；

    （2）过点作圆的切线，交于点.若，求的值；

    （3）在（2）的条件下，当时，求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

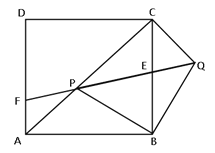
    【题目】如图，等腰Rt△BPQ的顶点P在正方形ABCD的对角线AC上（P与AC不重合），∠PBQ=90°，QP与BC交于E,QP延长线交AD于F，连CQ.

    (1)①求证：AP=CQ ；

    ②求证：

    (2)当时，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某网店销售某款童装，每件售价60元，每星期可卖300件，为了促销，该网店决定降价销售．市场调查反映：每降价1元，每星期可多卖30件．已知该款童装每件成本价40元，设该款童装每件售价x元，每星期的销售量为y件．

    （1）求y与x之间的函数关系式；

    （2）当每件售价定为多少元时，每星期的销售利润最大，最大利润多少元？

    （3）若该网店每星期想要获得不低于6480元的利润，每星期至少要销售该款童装多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

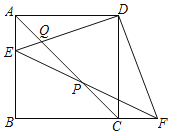
    【题目】如图，在边长为4的正方形ABCD中，∠EDF＝90°，点E在边AB上且不与点A重合，点F在边BC的延长线上，DE交AC于Q，连接EF交AC于P

    （1）求证：△ADE≌△CDF；

    （2）求证：PE＝PF；

    （3）当AE＝1时，求PQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店购进一批单价为16元的日用品,销售一段时间后,为了获取更多利润, 商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件; 若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x( 元/件)的一次函数.

    (1)试求y与x之间的函数关系式;

    (2)在商品不积压,且不考虑其他因素的条件下,问销售价格为多少时,才能使每月获得最大利润?每月的最大利润是多少?(总利润=总收入-总成本).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝ax2+bx+与y轴交于点A，与x轴交于点B、C，连结AB，以AB为边向右做平行四边形ABDE，点E落在抛物线上，点D落在x轴上，若抛物线的对称轴恰好经过点D，且∠ABD＝60°，则平行四边形的面积为_____．

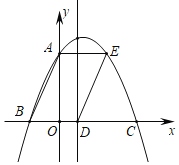
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,二次函数的图象与轴正半轴相交于A、B两点,与轴相交于点C,对称轴为直线且OA=OC,则下列结论:①②③④关于的方程有一个根为其中正确的结论个数有（ ）

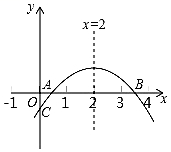
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    同步练习册答案