
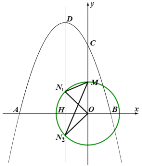
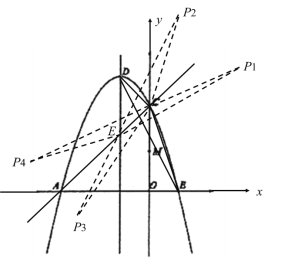
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点.
是抛物线的顶点.
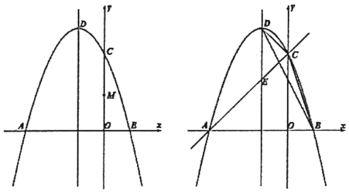
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 轴正半轴上的一点,
轴正半轴上的一点,![]() ,点
,点![]() 在对称轴左侧的抛物线上运动,直线
在对称轴左侧的抛物线上运动,直线![]() 交抛物线的对称轴于点
交抛物线的对称轴于点![]() ,连接
,连接![]() ,当
,当![]() 平分
平分![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)直线![]() 交对称轴于点
交对称轴于点![]() ,
,![]() 是坐标平面内一点,当
是坐标平面内一点,当![]() 与
与![]() 全等时,请直接写出点
全等时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)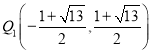 ,
,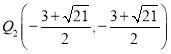 ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)用待定系数法,直接将AB代入解析式即可求解.
(2)由MN平分∠OMD,MD平行ON即可求出OM=ON=![]() ,继而得出N点坐标,由直线ON解析式即可求出与抛物线交点坐标Q即可.
,继而得出N点坐标,由直线ON解析式即可求出与抛物线交点坐标Q即可.
(3)由BCD三点的坐标可得△BCD三角形三边长,由CE坐标可得,△PCE和△ACD中CD=CE,则另两组边对应相等即可,设P点坐标为(x,y);利用勾股定理即列方程求解.
解:(1)∵抛物线![]() 经过
经过![]() ,
,![]() 两点,
两点,
∴![]() 解得:
解得:![]()
∴抛物线的解析式为:![]() .
.
(2)设对称轴与![]() 轴交于点
轴交于点![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
∴![]() ,
,
∴![]() ;
;![]() .
.
①当![]() 时,直线
时,直线![]() 解析式为:
解析式为:![]() ,
,
依题意得:![]() .
.
解得:![]() ,
,![]() .
.
∵点![]() 在对称轴左侧的抛物线上运动,
在对称轴左侧的抛物线上运动,
∴![]() 点纵坐标
点纵坐标![]() .
.
∴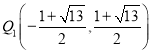 ;
;
②当![]() 时,直线
时,直线![]() 解析式为:
解析式为:![]() ,同理可求:
,同理可求:
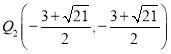 .
.
综上所述:点![]() 的坐标为:
的坐标为:
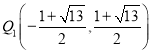 ,
,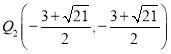
(3)若![]() 与
与![]() 全等,
全等,![]() 点有四个,坐标为
点有四个,坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.
由题意可知:![]() ,
,![]() ,
,![]()
![]() ,B(1,0),
,B(1,0),
![]() ,
,![]() ,
,![]() ,
,
![]() 直线AC经过
直线AC经过![]() ,
,![]() ,设AC的解析式为y=kx+b,
,设AC的解析式为y=kx+b,
将A和C代入,得![]() ,解得:
,解得:![]() ,
,
![]() 直线AC解析式为
直线AC解析式为![]() ,
,
![]() 抛物线对称轴为
抛物线对称轴为![]() ,而直线AC交对称轴于点
,而直线AC交对称轴于点![]() ,
,
![]() 坐标为
坐标为![]() ;
;
![]() ,
,
设![]() 点坐标为
点坐标为![]() ,
,
则![]() ,
,
则![]() ,
,
![]() ,若
,若![]() 与
与![]() 全等,有两种情况,
全等,有两种情况,
Ⅰ.![]() ,
,![]() ,即
,即![]() .
.
![]()
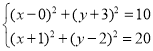 ,
,
解得: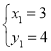 ,
,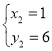 ,
,
即![]() 点坐标为
点坐标为![]() ,
,![]() .
.
Ⅱ.![]() ,
,![]() ,即
,即![]() .
.
![]()
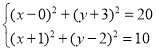 ,
,
解得: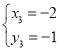 ,
,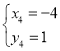 ,
,
即![]() 点坐标为
点坐标为![]() ,
,![]() .
.
故若△PCE与△ACD全等,P点有四个,坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
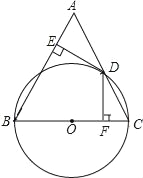
【题目】如图,在ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F,
①求证:ED是⊙O的切线;
②求证:DE2=BFAE;
③若DF=3![]() ,cosA=
,cosA=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,∠ACB=30°,将矩形ABCD绕点A旋转得到矩形AB′C′D′,使点B的对应点B′落在AC上,B′C′交AD于点E,在B′C′上取点F,使FB′=AB.
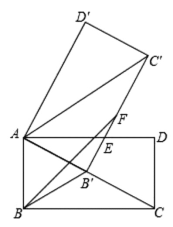
(1)求证:BB′= FB′;
(2)求∠FBB′的度数 ;
(3)已知AB=4,求△BFB′面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,以线段
上,以线段![]() 的长为半径的
的长为半径的![]() 与
与![]() 相切于点
相切于点![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,连接
,连接![]() 并延长交
并延长交![]() 延长线于点
延长线于点![]() .
.
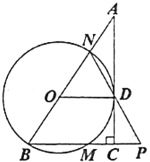
(1)求证:![]() ;
;
(2)已知![]() 的半径为5.
的半径为5.
①若![]() ,则
,则![]() __________;
__________;
②连接![]() ,当
,当![]() __________时,四边形
__________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七年级学生体育测试情况,以七年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)计算D级的学生人数,并把条形统计图补充完整;
(2)计算扇形统计图中A级所在的扇形的圆心角度数:
(3)若该校七年级有600名学生,请估计体育测试中B级学生人数约为多少人?
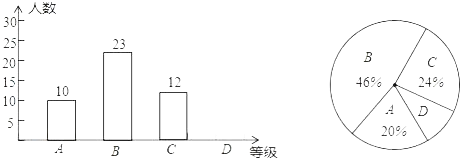
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情之下,中华儿女共抗时艰.重庆和湖北同饮长江水,为更好地驰援武汉,打赢防疫攻坚战,我市某公益组织收集社会捐献物资.甲、乙两人先后从![]() 地沿相同路线出发徒步前往
地沿相同路线出发徒步前往![]() 地进行物资捐献,甲出发1分钟后乙再出发,一段时间后乙追上甲,这时甲发现有东西落在
地进行物资捐献,甲出发1分钟后乙再出发,一段时间后乙追上甲,这时甲发现有东西落在![]() 地,于是原路原速返回
地,于是原路原速返回![]() 地去取(甲取东西的时间忽略不计),而乙继续前行,甲乙两人到达B地后原地帮忙.已知在整个过程中,甲乙均保持各自的速度匀速行走,甲、乙两人相距的路程
地去取(甲取东西的时间忽略不计),而乙继续前行,甲乙两人到达B地后原地帮忙.已知在整个过程中,甲乙均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分钟)之间的函数关系如图所示,则当乙到达
(分钟)之间的函数关系如图所示,则当乙到达![]() 地时,甲距
地时,甲距![]() 地的路程是_______米.
地的路程是_______米.
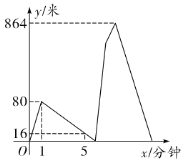
查看答案和解析>>
科目:初中数学 来源: 题型:
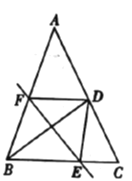
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的中点,线段
边的中点,线段![]() 的垂直平分线分别与边
的垂直平分线分别与边![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,连接
,连接![]() ,
,![]() .设
.设![]() ,
,![]() .给出以下结论:①
.给出以下结论:①![]() ;②
;②![]() 的面积为
的面积为![]() ;③
;③![]() 的周长为
的周长为![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确结论有_______(把你认为正确结论的序号都填上).
.其中正确结论有_______(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
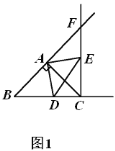
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在射线
在射线![]() 上(不与点
上(不与点![]() 、点
、点![]() 重合),将线段
重合),将线段![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,作射线
,作射线![]() 与射线
与射线![]() ,两射线交于点
,两射线交于点![]() .
.
(1)若点![]() 在线段
在线段![]() 上,如图1,请直接写出
上,如图1,请直接写出![]() 与
与![]() 的关系.
的关系.
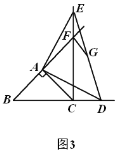
(2)若点![]() 在线段
在线段![]() 的延长线上,如图2,(1)中的结论还成立吗?请说明理由.
的延长线上,如图2,(1)中的结论还成立吗?请说明理由.

(3)在(2)的条件下,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com