已知直线y=2x+4与x轴、y轴的交点分别为A、B,y轴上点C的坐标为(0,2),在x轴的正半轴上找一点P,使以P、O、C为顶点的三角形与△AOB相似,则点P的坐标为 .
【答案】
分析:如图,A、B两点的坐标容易根据直线的解析式求出,所以OA、OB的长度也可以求出,而C的坐标已知,所以OC=2,而以P、O、C为顶点的三角形与△AOB相似有两种情况,其中OC可以和OA对应,也可以和OB对应,利用相似三角形的对应边成比例就可以求出OP的长度,也就求出了P的坐标.
解答: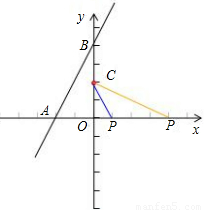
解:如图,
∵直线y=2x+4,
∴当x=0时,y=4;
当y=0时,x=-2.
∴A(-2,0),B(0,4),
∴OA=2,OB=4,
∵C的坐标为(0,2),
∴OC=2,
若以P、O、C为顶点的三角形与△AOB相似,
那么有两种情况:
①OC和OA对应,那么OP和OB对应,
∵OA=OC=2,
∴OP=OB=4,
∴P的坐标为(4,0);
②OC和OB对应,那么OP和OA对应,
∴
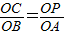
,
∴OP=1,
∴P的坐标为(1,0).
因此P的坐标为(4,0)或(1,0).
故填空答案:(4,0)或(1,0).
点评:此题把一次函数与相似三角形的性质与判定相结合,考查了同学们综合运用所学知识的能力,是一道综合性较好的题目.

 解:如图,
解:如图,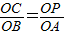 ,
,
