
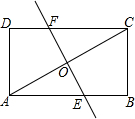
 如图,矩形ABCD中,对角线AC的中点为O,过O作EF⊥AC,分别交AB、DC于E、F,若AB=4,BC=2,那么线段EF的长为$\sqrt{5}$.
如图,矩形ABCD中,对角线AC的中点为O,过O作EF⊥AC,分别交AB、DC于E、F,若AB=4,BC=2,那么线段EF的长为$\sqrt{5}$. 分析 连接EC,设AE=EC=x,在RT△ECB中,求出EC,再在RT△ECO中求出EO,再利用全等三角形证明OE=OF即可解决问题.
解答 解: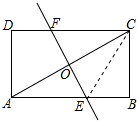 连接EC,
连接EC,
∵四边形ABCD是矩形,
∴∠B=90°,∵AB=4,BC=2,
∴AB=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∵AO=OC,EF⊥AC,
∴EA=EC,设EA=EC=x,在RT△ECB中,∵EC2=EB2+BC2,
∴x2=22+(4-x)2,
∴x=2.5,
在RT△EOC中,OE=$\sqrt{E{C}^{2}-O{C}^{2}}$=$\frac{\sqrt{5}}{2}$,
∵AB∥CD,
∴∠OCF=∠OAE,
在△OCF和△OAE中,
$\left\{\begin{array}{l}{∠OCF=∠OAE}\\{OC=OA}\\{∠FOC=∠AOE}\end{array}\right.$,
∴△OCF≌△OAE,
∴OF=OE,
∴EF=2OE=$\sqrt{5}$,
故答案为$\sqrt{5}$.
点评 本题考查矩形的性质、全等三角形的判定和性质、勾股定理、线段的垂直平分线的性质等知识,解题的关键是利用勾股定理求出EC的长,学会添加常用辅助线,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
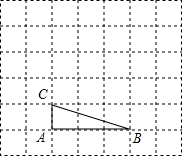 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
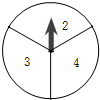 商场为了促销某件商品,设置了如图的一个转盘,它被分成了3个相同的扇形.各扇形分别标有数字2,3,4,指针的位置固定,该商品的价格由顾客自由转动此转盘两次来获取,每次转动后让其自由停止,记下指针所指的数字(指针指向两个扇形的交线时,当作右边的扇形),先记的数字作为价格的十位数字,后记的数字作为价格的个位数字,则顾客购买商品的价格不超过30元的概率是多少?
商场为了促销某件商品,设置了如图的一个转盘,它被分成了3个相同的扇形.各扇形分别标有数字2,3,4,指针的位置固定,该商品的价格由顾客自由转动此转盘两次来获取,每次转动后让其自由停止,记下指针所指的数字(指针指向两个扇形的交线时,当作右边的扇形),先记的数字作为价格的十位数字,后记的数字作为价格的个位数字,则顾客购买商品的价格不超过30元的概率是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
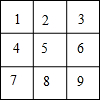 如图,九个小朋友用抽签的方式来确定各自的座位(如图中1~9这9个座位),小明第一个抽,抽到6号座位,小华第二个抽,那么小华抽到的座位恰好和小明的座位相邻的概率是$\frac{3}{8}$.
如图,九个小朋友用抽签的方式来确定各自的座位(如图中1~9这9个座位),小明第一个抽,抽到6号座位,小华第二个抽,那么小华抽到的座位恰好和小明的座位相邻的概率是$\frac{3}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
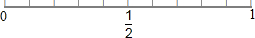 将下列事件发生的概率填在图中:(只填各事件的序号)
将下列事件发生的概率填在图中:(只填各事件的序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com