【题目】把一个图形绕着某一点旋转,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或,这个点叫做它们的.这两个图形在旋转后能重合的对应点叫做关于对称中心的.
科目：初中数学 来源： 题型：
【题目】问题提出：用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
问题探究：不妨假设能搭成
种不同的等腰三角形，为探究
之间的关系，我们可以从特殊入手，通过试验、观察、类比，最后归纳、猜测得出结论．
探究一：
（1）用3根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
此时，显然能搭成一种等腰三角形。所以，当
时，
（2）用4根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形
所以，当
时，
（3）用5根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形
所以，当
时，
（4）用6根相同的木棒搭成一个三角形，能搭成多少种不同的三角形？
若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形
所以，当
时，
综上所述，可得表①
| 3 | 4] | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二：
（1）用7根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三角形？
（仿照上述探究方法，写出解答过程，并把结果填在表②中）
（2）分别用8根、9根、10根相同的木棒搭成一个三角形，能搭成多少种不同的等腰三
角形？（只需把结果填在表②中）
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，……
解决问题：用
根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
（设分别等于
、
、
、
，其中
是整数，把结果填在表③中）
|
|
|
|
|
|
问题应用：用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（要求写出解答过程）其中面积最大的等腰三角形每个腰用了__________________根木棒。（只填结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，AC的垂直平分线分别交AB、AC于点D、E．
（1）若∠A = 40°，求∠DCB的度数．
（2）若AE=4，△DCB的周长为13，求△ABC的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解参加某运动会的2 000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题来说,下面说法正确的是( )
A.2 000名运动员是总体
B.每个运动员是个体
C.100名运动员是抽取的一个样本
D.100名运动员的年龄是抽取的一个样本
查看答案和解析>>
科目：初中数学 来源： 题型：
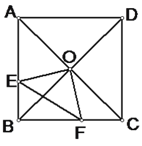
【题目】在正方形ABCD中，O是对角线的交点，过O作OE⊥OF，分别交AB、BC于E、F，若AE＝4，CF＝3，
（1）求证：OE=OF
（2）求 EF的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
