
分析 (1)利用两种树苗共计500棵,购买甲种树苗x棵,进而得出购买乙种树苗的棵数;
(2)利用甲种树苗每棵50元,乙种树苗每棵80元,进而表示出总费用求出即可;
(3)利用购买树苗的钱数不得超过34000元,得出不等式求出即可.
解答 解:(1)∵计划购买甲、乙两种树苗共计500棵,
设购买甲种树苗x棵,
∴购买乙种树苗为(500-x)棵;
(2)根据题意可得:50x+80(500-x)=28000,
解得;x=400,
则500-400=100(棵).
答:甲种树苗买了400棵,乙种树苗买了100棵;
(3)由题意可得:50x+80(500-x)≤34000,
解得:x≥200.
即购买甲种树苗不能少于200棵.
点评 此题主要考查了一元一次方程的应用以及一元一次不等式的应用,根据题意得出正确不等关系是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
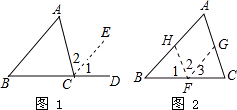
 将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )
将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )| A. | 135° | B. | 60° | C. | 50° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.0008=8×10-3 | B. | 0.0056=56×10-2 | ||
| C. | 19000=1.9×105 | D. | -0.00012=-1.2×10-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1000名运动员是总体 | B. | 抽取的100名运动员是样本 | ||
| C. | 样本容量是100 | D. | 每个运动员是个体 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com