
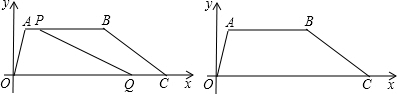
分析 (1)先由运动知,CQ=2t,BP=6-t,进而根据平行四边形得性质即可建立方程求解即可;
(2)先判断出Rt△BFC≌Rt△PEQ,再用CQ=EQ+EF+CF建立方程即可得出结论;
(3)先判断出CQ=CF+PB,进而建立方程即可得出结论;
(4)分三种情况讨论计算即可得出结论.
解答 解:∵A(1,3),B(7,3),
∴AB∥x轴,AB=7-1=6,
∵C(12,0),
∴OC=12,
设运动时间为t,(0≤t≤6)
(1)由运动知,AP=t,CQ=2t,
∴BP=AB-AP=6-t,
∵四边形BPQC为平行四边形,
∴BP=CQ,
∴6-t=2t,
∴t=2秒,
即:运动2秒后,四边形BPQC为平行四边形
(2)如图1,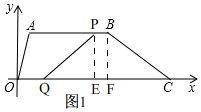
过点B作BF⊥OC,过点P作PE⊥OC,
∴四边形PEFB是矩形,
∴PB=EF,PE=BF,
∵B(7,3),
∴F(7,0),
∴CF=5,
∵四边形PBCQ是等腰梯形,
∴PQ=BC,
在Rt△BFC和Rt△PEQ中,$\left\{\begin{array}{l}{BC=PQ}\\{BF=PE}\end{array}\right.$,
∴Rt△BFC≌Rt△PEQ,
∴EQ=CF=5,
∴CQ=EQ+EF+CF,
由运动知,AP=t,CQ=2t,
∴EF=PB=6-t,
∴2t=5+6-t+5,
∴t=$\frac{16}{3}$,
即:运动$\frac{16}{3}$秒后,四边形BPQC为等腰梯形
(3)如图2,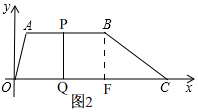 过点B作BF⊥OC,
过点B作BF⊥OC,
∵四边形PBCQ是直角梯形,
∴四边形BFQP是矩形,
∴FQ=PB,
∴CQ=CF+FQ=CF+PB,
由(2)知,CF=5,
由(1)知,PB=6-t,
∴2t=5+6-t,
∴t=$\frac{11}{3}$,
即:运动$\frac{11}{3}$秒后,四边形BPQC为直角梯形;
(4)设运动时间为t,
∴AP=t,CQ=2t,
∴OQ=12-t,
∴P(t+1,3),Q(12-t,0),
∴B(7,3),
∴BP2=(6-t)2=t2-12t+36,PQ2=(t+1-12+t)2+9=4t2-44t+130,BQ2=(12-t-7)2+9=t2-10t+34,
∵△QPB为等腰三角形,
∴①当BP=BQ时,t2-12t+36=t2-10t+34,
∴t=1,
②当BP=PQ时,t2-12t+36=4t2-44t+130,
此方程无解;
③当BQ=PQ时,4t2-44t+130=t2-10t+34,
∴t=$\frac{27}{4}$(舍)或t=$\frac{15}{4}$,
即:运动1秒或$\frac{15}{4}$秒后,△QPB为等腰三角形.
点评 此题是四边形综合题,主要考查了平行四边形的性质,等腰梯形和直角梯形的性质,等腰三角形得性质,解本题的关键是用方程的思想思考问题,是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:选择题
| A. | 如果线段AB和A′B′关于某条直线对称,那么AB=A′B′ | |
| B. | 如果点A和点A′到直线l的距离相等,A和A′关于直线l对称 | |
| C. | 如果AB=A′B′,且直线MN垂直平分AA′那么线段AB和A′B′关于直线MN对称 | |
| D. | 如果在直线MN两旁的两个图形能够完全重合,那么这两个图形关于直线MN对称 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,菱形ABCD中,AC与BD相交于点O,若AC=m,BD=n.
如图,菱形ABCD中,AC与BD相交于点O,若AC=m,BD=n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com