
分析 (1)由题意二次函数的图象的对称轴为x=2,函数的最小值为3,可设二次函数为:y=a(x-2)2+3,且函数过点(1,5)代入函数的解析式求出a值,从而求出二次函数的解析式.
(2)根据与x轴的两个交点的坐标,设出二次函数交点式解析式y=a(x-1)(x+3),然后把点(-1,4)的坐标代入计算求出a的值,即可得到二次函数解析式.
解答 解:(1)∵二次函数的图象的对称轴为x=2,函数的最小值为3,
∴可设函数解析式为:y=a(x-2)2+3,
∵函数图象经过点(1,5),
∴a×1+3=5,
∴a=2,
∴二次函数的表达式为:y=2(x-2)2+3,
即y=2x2-8x+11;
(2)∵二次函数的图象交x轴于(-3,0)、(1,0),
∴设该二次函数的解析式为:y=a(x-1)(x+3)(a≠0).
将x=-1,y=4代入,得6=a(-1-1)(-1+3),
解得a=-$\frac{3}{2}$,
∴抛物线的解析式为y=-$\frac{3}{2}$(x-1)(x+3),
即y=-$\frac{3}{2}$x2-3x+$\frac{9}{2}$.
点评 本题考查了待定系数法求二次函数解析式,利用待定系数法求二次函数解析式时,注意合理利用抛物线解析式的三种形式.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
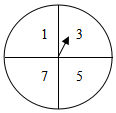 A超市在一次周年庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖机会,抽奖规则如下:将如图所示的图形转盘平均分成四个扇形,分别标上1,3,5,7四个数字,抽奖者连续转动转盘两次,当每次停止后指针所指扇形内的数为每次所得数(若指针指在分界处重转),当两次所得数字之和为2时,返现金20元,当两次所得数字之和为4时,返现金10元,当两次所得数字之和为6时,返现金5元.
A超市在一次周年庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖机会,抽奖规则如下:将如图所示的图形转盘平均分成四个扇形,分别标上1,3,5,7四个数字,抽奖者连续转动转盘两次,当每次停止后指针所指扇形内的数为每次所得数(若指针指在分界处重转),当两次所得数字之和为2时,返现金20元,当两次所得数字之和为4时,返现金10元,当两次所得数字之和为6时,返现金5元.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平面直角坐标系中,已知A(0,4)、B(1,0)、C(4,0),D为线段BC上的动点,以AD为边向右侧作正方形ADEF,连CF交DE于P,则CP的最大值为1.
在平面直角坐标系中,已知A(0,4)、B(1,0)、C(4,0),D为线段BC上的动点,以AD为边向右侧作正方形ADEF,连CF交DE于P,则CP的最大值为1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com