
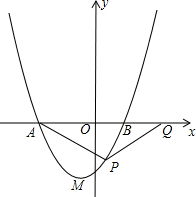
 ШчЭМЃЌХзЮяЯпy=-$\frac{1}{2}$x2+mx+nгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпЕФЖдГЦжсНЛxжсгкЕуDЃЌвбжЊAЃЈ-1ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЎ
ШчЭМЃЌХзЮяЯпy=-$\frac{1}{2}$x2+mx+nгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпЕФЖдГЦжсНЛxжсгкЕуDЃЌвбжЊAЃЈ-1ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЎЗжЮі ЃЈ1ЃЉжБНгАбAЕуКЭCЕузјБъДњШыy=-$\frac{1}{2}$x2+mx+nЕУmЁЂnЕФЗНГЬзщЃЌШЛКѓНтЗНГЬзщЧѓГіmЁЂnМДПЩЕУЕНХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉЯШРћгУХзЮяЯпЖдГЦжсЗНГЬЧѓГіХзЮяЯпЕФЖдГЦжсЮЊжБЯпx=-$\frac{3}{2}$ЃЌдђDЃЈ$\frac{3}{2}$ЃЌ0ЃЉЃЌдђРћгУЙДЙЩЖЈРэМЦЫуГіCD=$\frac{5}{2}$ЃЌШЛКѓЗжРрЬжТлЃКШчЭМ1ЃЌЕБCP=CDЪБЃЌРћгУЕШбќШ§НЧаЮЕФаджЪвзЕУP1ЃЈ$\frac{3}{2}$ЃЌ4ЃЉЃЛЕБDP=DCЪБЃЌвзЕУP2ЃЈ$\frac{3}{2}$ЃЌ$\frac{5}{2}$ЃЉЃЌP3ЃЈ$\frac{3}{2}$ЃЌ-$\frac{5}{2}$ЃЉЃЛ
ЃЈ3ЃЉЯШИљОнХзЮяЯпгыxжсЕФНЛЕуЮЪЬтЧѓГіBЃЈ4ЃЌ0ЃЉЃЌдйРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпBCЕФНтЮіЪНЮЊy=-$\frac{1}{2}$x+2ЃЌРћгУвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїКЭЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїЃЌЩшEЃЈxЃЌ-$\frac{1}{2}$x+2ЃЉЃЈ0ЁмxЁм4ЃЉЃЌдђFЃЈxЃЌ-$\frac{1}{2}$x2+$\frac{3}{2}$x+2ЃЉЃЌдђFE=-$\frac{1}{2}$x2+2xЃЌгЩгкЁїBEFКЭЁїCEFЙВЕзБпЃЌИпЕФКЭЮЊ4ЃЌдђSЁїBCF=SЁїBEF+SЁїCEF=$\frac{1}{2}$•4•EF=-x2+4xЃЌМгЩЯSЁїBCD=$\frac{5}{2}$ЃЌЫљвдSЫФБпаЮCDBF=SЁїBCF+SЁїBCD=-x2+4x+$\frac{5}{2}$ЃЈ0ЁмxЁм4ЃЉЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪЧѓЫФБпаЮCDBFЕФУцЛ§зюДѓЃЌВЂЕУЕНДЫЪБEЕузјБъЃЎ
НтД№ НтЃКЃЈ1ЃЉАбAЃЈ-1ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉДњШыy=-$\frac{1}{2}$x2+mx+nЕУ$\left\{\begin{array}{l}{-\frac{1}{2}-m+n=0}\\{n=2}\end{array}\right.$ЃЌНтЕУ$\left\{\begin{array}{l}{m=\frac{3}{2}}\\{n=2}\end{array}\right.$ЃЌ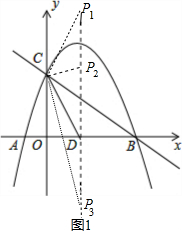
ЁрХзЮяЯпНтЮіЪНЮЊy=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2ЃЛ
ЃЈ2ЃЉДцдкЃЎ
ХзЮяЯпЕФЖдГЦжсЮЊжБЯпx=-$\frac{\frac{3}{2}}{2ЁСЃЈ-\frac{1}{2}ЃЉ}$=$\frac{3}{2}$ЃЌ
дђDЃЈ$\frac{3}{2}$ЃЌ0ЃЉЃЌ
ЁрCD=$\sqrt{O{D}^{2}+O{C}^{2}}$=$\sqrt{ЃЈ\frac{3}{2}ЃЉ^{2}+{2}^{2}}$=$\frac{5}{2}$ЃЌ
ШчЭМ1ЃЌЕБCP=CDЪБЃЌдђP1ЃЈ$\frac{3}{2}$ЃЌ4ЃЉЃЛ
ЕБDP=DCЪБЃЌдђP2ЃЈ$\frac{3}{2}$ЃЌ$\frac{5}{2}$ЃЉЃЌP3ЃЈ$\frac{3}{2}$ЃЌ-$\frac{5}{2}$ЃЉЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФPЕузјБъЮЊЃЈ$\frac{3}{2}$ЃЌ4ЃЉЛђЃЈ$\frac{3}{2}$ЃЌ$\frac{5}{2}$ЃЉЛђЃЈ$\frac{3}{2}$ЃЌ-$\frac{5}{2}$ЃЉЃЛ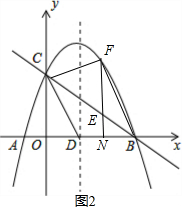
ЃЈ3ЃЉЕБy=0ЪБЃЌ=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0ЃЌНтЕУx1=-1ЃЌx2=4ЃЌдђBЃЈ4ЃЌ0ЃЉЃЌ
ЩшжБЯпBCЕФНтЮіЪНЮЊy=kx+bЃЌ
АбBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉДњШыЕУ$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$ЃЌНтЕУ$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$ЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊy=-$\frac{1}{2}$x+2ЃЌ
ЩшEЃЈxЃЌ-$\frac{1}{2}$x+2ЃЉЃЈ0ЁмxЁм4ЃЉЃЌдђFЃЈxЃЌ-$\frac{1}{2}$x2+$\frac{3}{2}$x+2ЃЉЃЌ
ЁрFE=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2-ЃЈ-$\frac{1}{2}$x+2ЃЉ=-$\frac{1}{2}$x2+2xЃЌ
ЁпSЁїBCF=SЁїBEF+SЁїCEF=$\frac{1}{2}$•4•EF=2ЃЈ-$\frac{1}{2}$x2+2xЃЉ=-x2+4xЃЌ
ЖјSЁїBCD=$\frac{1}{2}$ЁС2ЁСЃЈ4-$\frac{3}{2}$ЃЉ=$\frac{5}{2}$ЃЌ
ЁрSЫФБпаЮCDBF=SЁїBCF+SЁїBCD
=-x2+4x+$\frac{5}{2}$ЃЈ0ЁмxЁм4ЃЉЃЌ
=-ЃЈx-2ЃЉ2+$\frac{13}{2}$
ЕБx=2ЪБЃЌSЫФБпаЮCDBFгазюДѓжЕЃЌзюДѓжЕЮЊ$\frac{13}{2}$ЃЌДЫЪБEЕузјБъЮЊЃЈ2ЃЌ1ЃЉЃЎ
ЕуЦР БОЬтПМВщСЫЖўДЮКЏЪ§ЕФзлКЯЬтЃКЪьСЗеЦЮеЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїЁЂвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїКЭЖўДЮКЏЪ§ЕФаджЪЃЛЛсРћгУД§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§ЕФНтЮіЪНЃЛРэНтзјБъгыЭМаЮаджЪЃЛСщЛюгІгУШ§НЧаЮЕФУцЛ§ЙЋЪНЃЛбЇЛсдЫгУЗжРрЬжТлЕФЫМЯыНтОіЪ§бЇЮЪЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
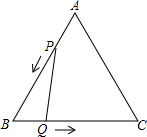 ШчЭМЃЌвбжЊЁїABCЪЧБпГЄЮЊ3cmЕФЕШБпШ§НЧаЮЃЌЖЏЕуPЃЌQЭЌЪБДгAЃЌBСНЕуГіЗЂЃЌЗжБ№биABЃЌBCЗНЯђдШЫйвЦЖЏЃЌЫќУЧЕФЫйЖШЖМЪЧ1cm/sЃЌЕБЕуPЕНДяЕуBЪБЃЌPЃЌQСНЕуЖМЭЃжЙдЫЖЏЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtЃЈsЃЉЃЎНтД№ЯТСаЮЪЬтЃК
ШчЭМЃЌвбжЊЁїABCЪЧБпГЄЮЊ3cmЕФЕШБпШ§НЧаЮЃЌЖЏЕуPЃЌQЭЌЪБДгAЃЌBСНЕуГіЗЂЃЌЗжБ№биABЃЌBCЗНЯђдШЫйвЦЖЏЃЌЫќУЧЕФЫйЖШЖМЪЧ1cm/sЃЌЕБЕуPЕНДяЕуBЪБЃЌPЃЌQСНЕуЖМЭЃжЙдЫЖЏЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtЃЈsЃЉЃЎНтД№ЯТСаЮЪЬтЃКВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 22Лђ23 | BЃЎ | 23Лђ24 | CЃЎ | 24Лђ25 | DЃЎ | 25Лђ26 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
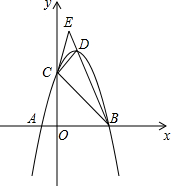 ШчЭМЃЌвбжЊХзЮяЯпy=-x2+bx+cНЛxжсгкAЃЈ-1ЃЌ0ЃЉЁЂBЃЈ3ЃЌ0ЃЉСНЕуЃЌНЛyжсгкCЕуЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЌСЌНгACЁЂBDВЂбгГЄНЛгкЕуEЃЌСЌНгBCЃЌCDЃЎ
ШчЭМЃЌвбжЊХзЮяЯпy=-x2+bx+cНЛxжсгкAЃЈ-1ЃЌ0ЃЉЁЂBЃЈ3ЃЌ0ЃЉСНЕуЃЌНЛyжсгкCЕуЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЌСЌНгACЁЂBDВЂбгГЄНЛгкЕуEЃЌСЌНгBCЃЌCDЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 вбжЊХзЮяЯпy=x2+2ЃЈm+1ЃЉx+4mЃЌЫќгыxжсЗжБ№НЛгкдЕуOзѓВрЕФЕуAЃЈx1ЃЌ0ЃЉКЭгвВрЕФЕуBЃЈx2ЃЌ0ЃЉЃЎ
вбжЊХзЮяЯпy=x2+2ЃЈm+1ЃЉx+4mЃЌЫќгыxжсЗжБ№НЛгкдЕуOзѓВрЕФЕуAЃЈx1ЃЌ0ЃЉКЭгвВрЕФЕуBЃЈx2ЃЌ0ЃЉЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com