
【题目】(2016广西省南宁市第23题)已知四边形ABCD是菱形,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB,DC相交于点E,F,且∠EAF=60°.
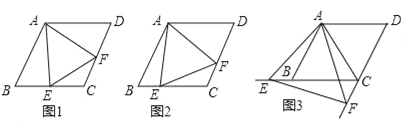
(1)如图1,当点E是线段CB的中点时,直接写出线段AE,EF,AF之间的数量关系;
(2)如图2,当点E是线段CB上任意一点时(点E不与B、C重合),求证:BE=CF;
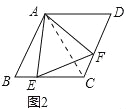
(3)如图3,当点E在线段CB的延长线上,且∠EAB=15°时,求点F到BC的距离.
【答案】(1)、AE=EF=AF;(2)、证明过程见解析;(3)、3-![]()
【解析】
试题分析:(1)、结论AE=EF=AF.只要证明AE=AF即可证明△AEF是等边三角形;(2)、欲证明BE=CF,只要证明△BAE≌△CAF即可;(3)、过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,根据FH=CFcos30°,因为CF=BE,只要求出BE即可解决问题.
试题解析:(1)、结论AE=EF=AF.
理由:如图1中,连接AC, ∵四边形ABCD是菱形,∠B=60°, ∴AB=BC=CD=AD,∠B=∠D=60°,
∴△ABC,△ADC是等边三角形, ∴∠BAC=∠DAC=60° ∵BE=EC, ∴∠BAE=∠CAE=30°,AE⊥BC,
∵∠EAF=60°, ∴∠CAF=∠DAF=30°, ∴AF⊥CD, ∴AE=AF(菱形的高相等),
∴△AEF是等边三角形, ∴AE=EF=AF.
(2)、如图2中,∵∠BAC=∠EAF=60°, ∴∠BAE=∠CAE,
在△BAE和△CAF中,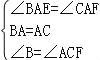 , ∴△BAE≌△CAF, ∴BE=CF.
, ∴△BAE≌△CAF, ∴BE=CF.
(3)、过点A作AG⊥BC于点G,过点F作FH⊥EC于点H, ∵∠EAB=15°,∠ABC=60°, ∴∠AEB=45°,
在RT△AGB中,∵∠ABC=60°AB=4, ∴BG=2,AG=2![]() ,在RT△AEG中,∵∠AEG=∠EAG=45°,
,在RT△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2![]() , ∴EB=EG﹣BG=2
, ∴EB=EG﹣BG=2![]() ﹣2, ∵△AEB≌△AFC,
﹣2, ∵△AEB≌△AFC,
∴AE=AF,EB=CF=2![]() ﹣2,∠AEB=∠AFC=45°, ∵∠EAF=60°,AE=AF, ∴△AEF是等边三角形,
﹣2,∠AEB=∠AFC=45°, ∵∠EAF=60°,AE=AF, ∴△AEF是等边三角形,
∴∠AEF=∠AFE=60° ∵∠AEB=45°,∠AEF=60°, ∴∠CEF=∠AEF﹣∠AEB=15°,
在RT△EFH中,∠CEF=15°, ∴∠EFH=75°, ∵∠AFE=60°, ∴∠AFH=∠EFH﹣∠AFE=15°,
∵∠AFC=45°,∠CFH=∠AFC﹣∠AFH=30°, 在RT△CHF中,∵∠CFH=30°,CF=2![]() ﹣2,
﹣2,
∴FH=CFcos30°=(2![]() ﹣2)
﹣2)![]() =3﹣
=3﹣![]() . ∴点F到BC的距离为3﹣
. ∴点F到BC的距离为3﹣![]() .
.



科目:初中数学 来源: 题型:
【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
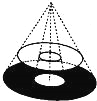
A.0.324πm2B.0.288πm2C.1.08πm2D.0.72πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些数排列成下表:
第1列 | 第2列 | 第3列 | 第4列 | |
第1行 | 1 | 4 | 5 | 10 |
第2行 | 4 | 8 | 10 | 12 |
第3行 | 9 | 12 | 15 | 14 |
|
|
|
|
|
试探索:(请直接写出答案)
(1)第10行第2列的数是多少?
(2)数81所在的行和列分别是多少?
(3)数100所在的行和列分别是多少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读后回答问题:
计算(-![]() )÷(-15)×(-
)÷(-15)×(-![]() )
)
解:原式=-![]() ÷[(-15)×(-
÷[(-15)×(-![]() )] ①
)] ①
=-![]() ÷1 ②
÷1 ②
=-![]() ③
③
()上述的解法是否正确?答:_________________________
若有错误,在哪一步?答:_________________________(填代号)
错误的原因是:___________________________________
(2)这个计算题的正确答案应该是:______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值
(1)-(9x3-4x2+5)-(-3-8x3+3x2),其中x=-2;
(2)5xy﹣[x2+4xy﹣y2﹣(x2+2xy﹣2y2)]其中![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com