
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出的下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出的下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,可得△>0,所以b2-4ac>0,据此判断即可.
②根据对称轴是x=1,可得-$\frac{b}{2a}$=1,所以2a+b=0,据此判断即可.
③根据函数的图象,可得x=-2时,y<0,所以4a-2b+c<0,据此判断即可.
④首先根据x=-1时,y=0,可得a-b+c=0;然后根据2a+b=0,即可推得3b=2c.
解答 解:∵二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,
∴△>0,
∴b2-4ac>0,
∴结论①正确.
∵-$\frac{b}{2a}$=1,
∴2a+b=0,
∴结论②不正确.
∵x=-2时,y<0,
∴4a-2b+c<0,
∴结论③不正确.
∵x=-1时,y=0,
∴a-b+c=0,
又∵2a+b=0,
∴-$\frac{b}{2}-b$+c=0,
∴3b=2c,
∴结论④正确.
综上,可得
正确的结论个数是2个:①④.
故选:B.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 中位数 | C. | 极差 | D. | 众数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
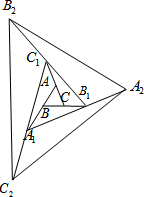 如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2015,最少经过( )次操作.
如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2015,最少经过( )次操作.| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,在三角形内裁剪正方形,使正方形四个顶点恰好在三角形的边上,共有两种裁法:
已知:Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c,在三角形内裁剪正方形,使正方形四个顶点恰好在三角形的边上,共有两种裁法:查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 明天我市降雨的概率是60%,指的是有60%的时间在下雨 | |
| B. | 样本的方差可以近似地反映总体的分布规律 | |
| C. | 若一组数据2,3,5,a的平均数是3,则这组数据的众数和中位数都是3 | |
| D. | 数据2,5,4,9的方差是6.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com