
| A. | 24 | B. | 24或8$\sqrt{5}$ | C. | 48或16$\sqrt{5}$ | D. | 8$\sqrt{5}$ |
分析 由x2-16x+60=0,可利用因式分解法求得x的值,然后分别从x=6时,是等腰三角形;与x=10时,是直角三角形去分析求解即可求得答案.
解答  解:∵x2-16x+60=0,
解:∵x2-16x+60=0,
∴(x-6)(x-10)=0,
解得:x1=6,x2=10,
当x=6时,则三角形是等腰三角形,如图①,AB=AC=6,BC=8,AD是高,
∴BD=4,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=2$\sqrt{5}$,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×8×2$\sqrt{5}$=8$\sqrt{5}$;
当x=10时,如图②,AC=6,BC=8,AB=10,
∵AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°,
S△ABC=$\frac{1}{2}$BC•AC=$\frac{1}{2}$×8×6=24.
∴该三角形的面积是:24或8$\sqrt{5}$.
故选:B.
点评 本题考查的是利用因式分解法解一元二次方程,等腰三角形的性质,勾股定理及其逆定理,解答此题时要注意分类讨论,不要漏解.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:选择题
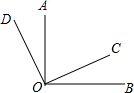 如图所示,∠AOB是直角,∠COD也是直角,∠AOC=65°,那么∠BOD的度数是( )
如图所示,∠AOB是直角,∠COD也是直角,∠AOC=65°,那么∠BOD的度数是( )| A. | 90°+65° | B. | 90°+2×65° | C. | 180°-65° | D. | 180°-2×65° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平面直角坐标系内xOy中,过双曲线y=$\frac{6}{x}$(x>0)上动点A分别作x轴,y轴的垂线段AB,AC,线段AB,AC与双曲线y=$\frac{k}{x}$(x>,0<k<6)分别交于E,F,记△OEF面积S1,记△AEF的面积为S2,则S=S1-S2的最大值为$\frac{3}{2}$.
在平面直角坐标系内xOy中,过双曲线y=$\frac{6}{x}$(x>0)上动点A分别作x轴,y轴的垂线段AB,AC,线段AB,AC与双曲线y=$\frac{k}{x}$(x>,0<k<6)分别交于E,F,记△OEF面积S1,记△AEF的面积为S2,则S=S1-S2的最大值为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,点P为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
如图,在平面直角坐标系中,点P为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )| A. | -2.5和-3之间 | B. | -3和-3.5之间 | C. | -3.5和-4之间 | D. | -4和-4.5 之间 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 肯定没有同一个班级的学生 | |
| B. | 可能有两名同学在一班级,但可能很小 | |
| C. | 至少有三名学生在同一个班级 | |
| D. | 至少有两名学生在同一个班级 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com