
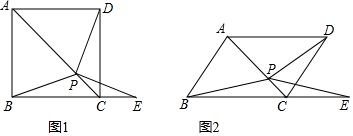
分析 (1)根据正方形的性质得到BC=DC,∠BCP=∠DCP=45°,证明△BCP≌△DCP;
(2)根据全等三角形的性质得到∠CBP=∠CDP,根据等腰三角形的性质得到∠CBP=∠E,证明∠DPE=∠DCE=90°,得到答案;
(3)根据菱形的性质、仿照(2)的证明方法解答即可.
解答 (1)证明:在正方形ABCD中,BC=DC,∠BCP=∠DCP=45°,
在△BCP和△DCP中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCP=∠DCP}\\{PC=PC}\end{array}\right.$,
∴△BCP≌△DCP(SAS);
(2)证明:由(1)知,△BCP≌△DCP,
∴∠CBP=∠CDP,
∵PE=PB,
∴∠CBP=∠E,
∴∠DPE=∠DCE=90°,
∴∠DPE=∠ABC;
(3)解:在菱形ABCD中,BC=DC,∠BCP=∠DCP,
在△BCP和△DCP中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCP=∠DCP}\\{PC=PC}\end{array}\right.$,
∴△BCP≌△DCP(SAS),
∴∠CBP=∠CDP,
∵PE=PB,
∴∠CBP=∠E,
∴∠DPE=∠DCE,
∵AB∥CD,
∴∠DCE=∠ABC,
∴∠DPE=∠ABC=56°,
故答案为:56.
点评 本题考查的是正方形的性质、菱形的性质、全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理、正方形和菱形的性质是解题的关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2>0 | B. | y1>0>y2 | C. | 0>y1>y2 | D. | y2>0>y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
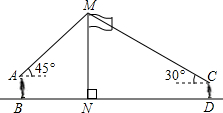 如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小明的眼睛与地面的距离AB是1.7m,看旗杆顶部M的仰角为45°,小红的眼睛与地面的距离CD是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.【参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数】
如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小明的眼睛与地面的距离AB是1.7m,看旗杆顶部M的仰角为45°,小红的眼睛与地面的距离CD是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.【参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,结果保留整数】查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com