Question

（2013年浙江义乌4分）如图，直线l₁⊥x轴于点A（2，0），点B是直线l₁上的动点．直线l₂：y=x+1交l₁于点C，过点B作直线l₃垂直于l₂，垂足为D，过点O，B的直线l₄交l ₂于点E．当直线l₁，l₂，l₃能围成三角形时，设该三角形面积为S₁，当直线l₂，l₃，l₄能围成三角形时，设该三角形面积为S₂．

（1）若点B在线段AC上，且S₁=S₂，则B点坐标为      ；

（2）若点B在直线l₁上，且S₂=S₁，则∠BOA的度数为      ．

 

Answer 1

【答案】

（1）（2，0）；（2）15°或75°。

【解析】（1）设B的坐标是（2，m），则△BCD是等腰直角三角形。

∵，∴。

∴。

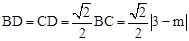设直线l₄的解析式是y=kx，则2k=m，解得：。        

∴直线l₄的解析式是。

根据题意得：，解得：。

∴E的坐标是（，）。

∴。

∴。

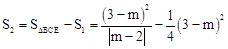当S₁=S₂时，。

解得：m=0，m=4（不在线段AC上，舍去），m=3（l₂和l₄重合，舍去）。

∴B的坐标是（2，0）。

（2）分三种情况：

①当点B在线段AC上时（如图1），

由S₂=S ₁得：。

解得：或（不在线段AC上，舍去），或m=3（l₂和l₄重合，舍去）。

∴AB=。

在OA上取点F，使OF=BF，连接BF，设OF=BF=x，

则AF=2－x，根据勾股定理，得，解得。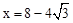

∴sin∠BFA=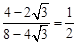。∴∠BFA=30°。∴∠BOA=15°。

②当点B在AC延长线上时（如图2），

此时，,

由S₂=S ₁得：。

解得：或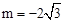（不在AC延长线上，舍去），或m=3（l₂和l₄重合，舍去）。

∴AB=。

在AB上取点G，使BG=OG，连接OG，设BG=OG=x，

则AG=，根据勾股定理，得，解得

∴sin∠OGA=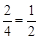。∴∠OGA =30°。∴∠OBA=15°。∴∠BOA=75°。

③当点B在CA延长线上时（如图3），

此时，,

由S₂=S ₁得：。

解得： m=3（l₂和l₄重合，舍去）。

∴此时满足条件的点B不存在。

综上所述，∠BOA的度数为15°或75°。

考点：一次函数综合题，单动点问题，直线上点的坐标与方程的关系，锐角三角函数定义，特殊角的三角函数值，分类的应用。