
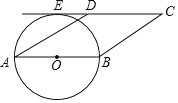
【题目】如图,在平行四边形ABCD中,AD=4,∠C=30°,⊙O与AD相交于点F,AB为⊙O的直径,⊙O与CD的延长线相切于点E,则劣弧FE的长为_________
【答案】![]()
【解析】
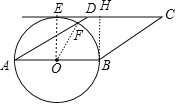
连接OE、OF,作BH⊥CD于H,如图,利用切线的性质得OE⊥CD,再利用平行四边形的性质得CD∥AB,∠A=∠C=30°,BC=AD=4,从而得到四边形OEHB为矩形,则BH=OE,计算出BH=2,然后求出∠EOF的度数后利用弧长公式求解.
连接OE、OF,作BH⊥CD于H,如图,
∵CD为![]() 切线,
切线,
∴OE⊥CD,
∵四边形ABCD为平行四边形,
∴CD∥AB,∠A=∠C=30°,BC=AD=4,
∴OE⊥AB,
易得四边形OEHB为矩形,
∴BH=OE,
在Rt△BCH中,BH=![]() BC=2,
BC=2,
∵OA=OC,
∴∠A=∠OCA=30°,
∴∠BOF=∠A+∠OFA=60°,
∴∠EOF=30°,
∴劣弧FE的长=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图平面直角坐标系中放置Rt△PEF,∠E=90°,EP=EF,△PEF绕点P(﹣1,﹣3)转动,PE、PF所在直线分别交y轴,x轴正半轴于点B(0,b),A(a,0),作矩形AOBC,双曲线y=![]() (k>0)经过C点,当a,b均为正整数时,k=_____.
(k>0)经过C点,当a,b均为正整数时,k=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线过x轴上两点A(9,0),C(﹣3,0),且与y轴交于点B(0,﹣12).
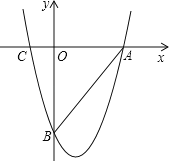
(1)求抛物线的解析式;
(2)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
①是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
②当点M运动到何处时,四边形CBNA的面积最大?求出此时点M的坐标及四边形CBNA面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,点A(0,4),B(﹣4,0),C(4,0).
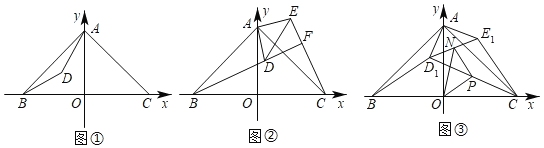
(1)如图①,若∠BAD=15°,AD=3,求点D的坐标;
(2)如图②,AD=2,将△ABD绕点A逆时针方向旋转得到△ACE,点B,D的对应点分别为C,E.连接DE,BD的延长线与CE相交于点F.
①求DE的长;
②证明:BF⊥CE.
(3)如图③,将(2)中的△ADE绕点A在平面内旋转一周,在旋转过程中点D,E的对应点分别为D1,E1,点N,P分别为D1E1,D1C的中点,请直接写出△OPN面积S的变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(n,![]() 2),B(
2),B(![]() 1,4)是一次函数y=kx+b和反比例函数y=
1,4)是一次函数y=kx+b和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
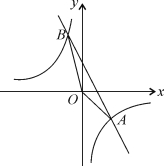
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
(3)直接写出kx+b>![]() 时,
时,![]() 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
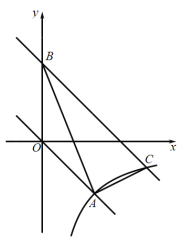
【题目】如图,在平面坐标系中,正比例函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像都经过点
的图像都经过点![]() .
.
(1)分别求出这两个函数的解析式;
(2)将直线OA向上平移3个单位后与![]() 轴交于点B,与反比例函数的图像在第四象限内的交点为C,连接
轴交于点B,与反比例函数的图像在第四象限内的交点为C,连接![]() ,求
,求![]() 的面积
的面积
(3)在(2)的条件下,反比例![]() 函数的图像上是否存在点D使得
函数的图像上是否存在点D使得![]() ?若存在直接写出点D的坐标;若不存在,请说明理由.
?若存在直接写出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作AC的平行线DE,交BA的延长线于点E.

求证:
(1)△ABC≌△DCB;
(2)DE·DC=AE·BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的单位正方形网格中,△ABC(点B与原点O重合)经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为( )
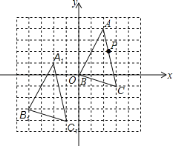
A.(1.4,1)B.(1.5,2)C.(1.6,1)D.(2.4,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com