
【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)

【答案】21m
【解析】试题分析:过点D作DH⊥BC于点M,得出四边形DECH是矩形,所以DH=EC,DE=HC,设BC的长度为xm,则BH=(x-5)m,由∠BDH=30°可以求出∠DBH=60°,进而表示出DH=![]() (x-5),然后表示出AC=
(x-5),然后表示出AC=![]() (x-5)-10,最后由BC= tan50°·AC列出方程,解出x即可.
(x-5)-10,最后由BC= tan50°·AC列出方程,解出x即可.
试题解析:
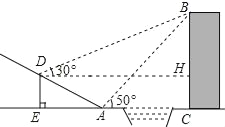
过点D作DH⊥BC于点M,
则四边形DHCE是矩形,DH=EC,DE=HC,
设BC的高度为xm,则BH=(x-5)m,
∵∠BDH=30°,
∴∠DBH=60°,
∴DH=BH·tan60°=![]() (x-5),
(x-5),
∴AC=EC-EA=![]() (x-5)-10,
(x-5)-10,
∵∠BAC=50°,
∴BC= tan50°·AC,
∴x=tan50°·[![]() (x-5)],
(x-5)],
解得:x≈21,
答:建筑物BC的高约为21m.


科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲,乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,根据图象信息回答下列问题:
(分钟)之间的函数关系如图所示,根据图象信息回答下列问题:

(1)图书馆与学校之间的距离为 米;
(2)当![]() 分钟时,甲乙两人相遇;
分钟时,甲乙两人相遇;
(3)乙的速度为 米/分钟;
(4)![]() 点的坐标为 .
点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,电线杆CD上的C处引拉线CE,CF固定电线杆,在离电线杆6米的B处安置测角仪(点B,E,D在同一直线上),在A处测得电线杆上C处的仰角为30°,已知测角仪的高AB=1.5米,BE=2.3米,求拉线CE的长,(精确到0.1米)参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73.
≈1.73.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的图象刻画了“龟兔再次赛跑”的故事(![]() 表示乌龟从起点出发所行的时间,
表示乌龟从起点出发所行的时间,![]() 表示乌龟所行的路程,
表示乌龟所行的路程,![]() 表示兔子所行的路程).
表示兔子所行的路程).
①“龟兔再次赛跑”的路程为______米;
②兔子比乌龟晚出发______分钟;
③乌龟在途中休息了______分钟;
④乌龟的速度是______米/分;
⑤兔子的速度是______米/分;
⑥兔子在距起点______米处追上乌龟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:
月均用水量(单位:吨 | 频数 | 频率 |
2≤x<3 | 4 | 0.08 |
3≤x<4 | a | b |
4≤x<5 | 14 | 0.28 |
5≤x<6 | 9 | c |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 5 | 0.1 |
合计 | d | 1.00 |

(1)b= ,c= ,并补全频数分布直方图;
(2)为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P= 吨;
(3)根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完二次根式一章后,小易同学看到这样一题:“函数![]() 中,自变量
中,自变量![]() 的取值范围是什么?”这个问题很简单,根据二次根式的性质很容易得到自变量
的取值范围是什么?”这个问题很简单,根据二次根式的性质很容易得到自变量![]() 的取值范围.联想到一次函数,小易想进一步研究这个函数的图象和性质.以下是他的研究步骤:
的取值范围.联想到一次函数,小易想进一步研究这个函数的图象和性质.以下是他的研究步骤:
第一步:函数![]() 中,自变量
中,自变量![]() 的取值范围是_____________.
的取值范围是_____________.
第二步:根据自变量取值范围列表:
| -1 | 0 | 1 | 2 | 3 | 4 | |
| 0 | 1 |
|
| 2 |
|
![]() __________.
__________.
第三步:描点画出函数图象.
在描点的时候,遇到了![]() ,
,![]() 这样的点,小易同学用所学勾股定理的知识,找到了画图方法,如图所示:
这样的点,小易同学用所学勾股定理的知识,找到了画图方法,如图所示:

你能否从中得到启发,在下面的![]() 轴上标出表示
轴上标出表示![]() 、
、![]() 、
、![]() 的点,并画出
的点,并画出![]() 的函数图象.
的函数图象.

第四步:分析函数的性质.
请写出你发现的函数的性质(至少写两条):
____________________________________________________________________________________________
____________________________________________________________________________________________
第五步:利用函数![]() 图象解含二次根式的方程和不等式.
图象解含二次根式的方程和不等式.
(1)请在上面坐标系中画出![]() 的图象,并估算方程
的图象,并估算方程![]() 的解.
的解.
(2)不等式![]() 的解是__________________.
的解是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,按以下步骤作图:①以点A为圆心,AB的长为半径作弧,交AD于点F;②分别以点F,B为圆心大于![]() FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )
FB的长为半径作弧,两弧在∠DAB内交于点G;③作射线AG,交边BC于点E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为( )

A.12B.20C.24D.48
查看答案和解析>>
科目:初中数学 来源: 题型:
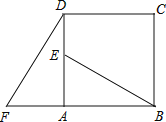
【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,
若AF=4,AB=7.
(1)旋转中心为______;旋转角度为______;
(2)DE的长度为______;
(3)指出BE与DF的位置关系如何?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com