
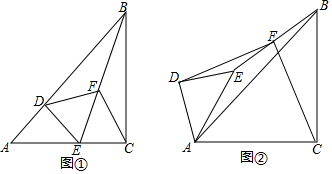
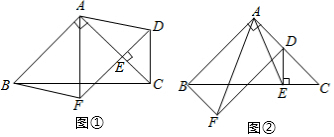
分析 (1)根据“直角三角形斜边上的中线等于斜边的一半”可知DF=BF=CF,根据∠DFE=2∠DCF,∠BFE=2∠BCF,得到∠EFD+∠EFB=2∠ABC=90°,进而得出DF⊥BF;
(2)延长DF至G使FG=DF,连接BG,CG,DC,先判定△BFG≌△EFD(SAS),得到∠FBG=∠FED,BG=ED,结合△ADE和△ACB都是等腰直角三角形,得出∠CBG=∠DAC,再判定△BCG≌△ACD(SAS),进而得到GC=DC,∠BCG=∠ACD,根据△DCG是等腰直角三角形,以及F是DG的中点,即可得到CF⊥DF且CF=DF.
解答 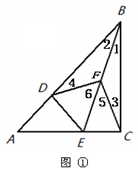 解:(1)CF=DF且CF⊥DF.理由如下:
解:(1)CF=DF且CF⊥DF.理由如下:
∵∠ADE=90°,
∴∠BDE=90°,
又∵∠BCE=90°,点F是BE的中点,
∴CF=DF=$\frac{1}{2}$BE=BF,
∴∠1=∠3,∠2=∠4,
∴∠5=∠1+∠3=2∠1,∠6=∠2+∠4=2∠2,
∴∠CFD=∠5+∠6=2(∠1+∠2)=2∠ABC,
又∵△ABC是等腰直角三角形,且∠ACB=90°,
∴∠ABC=45°,
∴∠CFD=90°,
∴CF=DF且CF⊥DF.
(2)(1)中的结论仍然成立.理由如下:
如图,延长DF至G使FG=DF,连接BG,CG,DC,
∵F是BE的中点,
∴BF=EF,
又∵∠BFG=∠EFD,GF=DF,
∴△BFG≌△EFD(SAS),
∴∠FBG=∠FED,BG=ED,
∴BG∥DE,
∵△ADE和△ACB都是等腰直角三角形,
∴DE=DA,∠DAE=∠DEA=45°,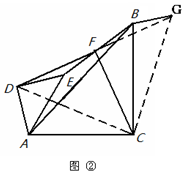
AC=BC,∠CAB=∠CBA=45°,
又∵∠CBG=∠EBG-∠EBA-∠ABC
=∠DEF-(180°-∠AEB-∠EAB)-45°
=∠DEF-180°+∠AEB+∠EAB-45°
=(∠DEF+∠AEB)+∠EAB-225°
=360°-∠DEA+∠EAB-225°
=360°-45°+∠EAB-225°
=90°+∠EAB,
而∠DAC=∠DAE+∠EAB+∠CAB
=45°+∠EAB+45°
=90°+∠EAB,
∴∠CBG=∠DAC,
又∵BG=ED,DE=DA,
∴BG=AD,
又∵BC=AC,
∴△BCG≌△ACD(SAS),
∴GC=DC,∠BCG=∠ACD,
∴∠DCG=∠DCB+∠BCG=∠DCB+∠ACD=∠ACB=90°,
∴△DCG是等腰直角三角形,
又∵F是DG的中点,
∴CF⊥DF且CF=DF.
点评 本题主要考查了旋转的性质,等腰直角三角形和全等三角形的判定与性质的运用.解题时需要作辅助线,构造全等三角形以及等腰直角三角形,掌握等腰直角三角形和全等三角形的性质及其判定定理是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了解今年全县2000名初二学生“创新能力大赛”的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据提供的信息,解答下列问题:
为了解今年全县2000名初二学生“创新能力大赛”的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 40 | 0.1 |
| 70≤x≤80 | 120 | n |
| 80≤x<90 | m | h |
| 90≤x<100 | 80 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
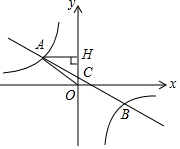 如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A,B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=6,sin∠AOH=$\frac{4}{5}$,点B的坐标为(m,-4).
如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A,B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=6,sin∠AOH=$\frac{4}{5}$,点B的坐标为(m,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com