
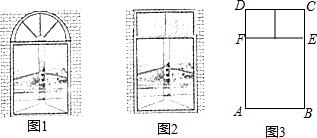
分析 (1)根据矩形和正方形的周长进行解答即可;
(2)设AB为xcm,利用二次函数的最值解答即可.
解答 解:(1)由已知可得:AD=$\frac{6-1-1-1-\frac{1}{2}}{2}=\frac{5}{4}$,
则S=1×$\frac{5}{4}=\frac{5}{4}$m2,
(2)设AB=xm,则AD=3-$\frac{7}{4}x$m,
∵$3-\frac{7}{4}x>0$,
∴$0<x<\frac{12}{7}$,
设窗户面积为S,由已知得:
$S=AB•AD=x(3-\frac{7}{4}x)=-\frac{7}{4}{x}^{2}+3x=-\frac{7}{4}(x-\frac{6}{7})^{2}+\frac{9}{7}$,
当x=$\frac{6}{7}$m时,且x=$\frac{6}{7}$m在$0<x<\frac{12}{7}$的范围内,${S}_{最大值}=\frac{9}{7}{m}^{2}>1.05{m}^{2}$,
∴与课本中的例题比较,现在窗户透光面积的最大值变大.
点评 此题考查二次函数的应用,关键是利用二次函数的最值解答.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:选择题
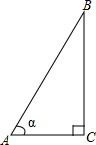 如图,为测量一棵与地面垂直的树BC的高度,在距离树的底端4米的A处,测得树顶B的仰角∠α=74°,则树BC的高度为( )
如图,为测量一棵与地面垂直的树BC的高度,在距离树的底端4米的A处,测得树顶B的仰角∠α=74°,则树BC的高度为( )| A. | $\frac{4}{tan74°}$米 | B. | 4sin74°米 | C. | 4tan74°米 | D. | 4cos74°米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
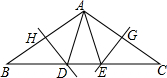 如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )
如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )| A. | $\frac{BD}{BC}$=$\frac{\sqrt{5}-1}{2}$ | B. | AD,AE将∠BAC三等分 | ||
| C. | △ABE≌△ACD | D. | S△ADH=S△CEG |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
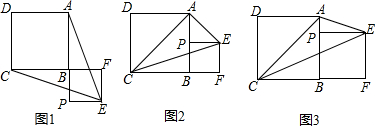
 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1-k2=4.
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1-k2=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com