
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
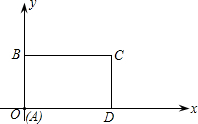 如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
如图所示,在平面直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=6.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动,当P点运动到D点时停止运动,矩形ABCD也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 细心观察图,认真分析各式,然后解答问题:
细心观察图,认真分析各式,然后解答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
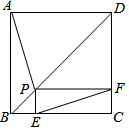 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=$\sqrt{2}$EC.其中正确结论的番号是( )
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=$\sqrt{2}$EC.其中正确结论的番号是( )| A. | ①②④⑤ | B. | ①②③④⑤ | C. | ①②④ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com