
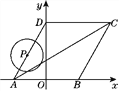
【题目】如图,菱形ABCD的顶点A,B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°,点A的坐标为(-2,0).
(1)求线段AD所在直线的表达式;
(2)动点P从点A出发,以每秒1个单位长度的速度,按照A→D→C→B→A的顺序在菱形的边上匀速运动一周,设运动时间为t秒.求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
【答案】(1)![]() ;(2) t=2,6,10或14.
;(2) t=2,6,10或14.
【解析】解:⑴∵点A的坐标为(-2,0),∠BAD=60°,∠AOD=90°,
∴OD=OA·tan60°=![]() ,
,
∴点D的坐标为(0,![]() ), 1分
), 1分
设直线AD的函数表达式为![]() ,
,
![]() ,解得
,解得![]() ,
,
∴直线AD的函数表达式为![]() . 3分
. 3分
⑵∵四边形ABCD是菱形,
∴∠DCB=∠BAD=60°,
∴∠1=∠2=∠3=∠4=30°,
AD=DC=CB=BA=4, 5分
如图所示:
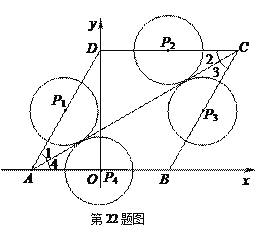
①点P在AD上与AC相切时,
AP1=2r=2,
∴t1="2." 6分
②点P在DC上与AC相切时,
CP2=2r=2,
∴AD+DP2=6,
∴t2="6." 7分
③点P在BC上与AC相切时,
CP3=2r=2,
∴AD+DC+CP3=10,
∴t3="10. " 8分
④点P在AB上与AC相切时,
AP4=2r=2,
∴AD+DC+CB+BP4=14,
∴t4=14,
∴当t=2、6、10、14时,以点P为圆心、以1为半径的圆与对角线AC相切. 9分


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养,随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成如图两幅统计图,请你结合图中信息解答问题.
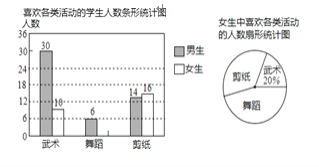
(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是 ;
(3)已知该校有1200名学生,请你根据样本估计全校学生中喜欢剪纸的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点D,E在AC的同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
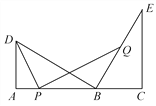
(1)求证:AC=AD+CE;
(2)若AD=3,AB=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q,当点P与A,B两点不重合时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(甲)是四边形纸片 ABCD,其中∠B=130°,∠D=50°.若将其右下角向内折出△PCR,恰使CP∥AB,RC∥AD,如图(乙)所示,则∠C=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
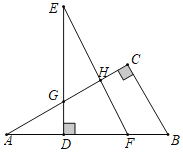
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB边上一点,DE⊥AB,且DE=AC,DE与AC交于点G,过点E作FE∥BC交AB于点F,交AC于点H.
(1)求证:△ABC≌△EFD;
(2)若∠EFD=55°,求∠DGH的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD绕点A逆时针旋转30°,得到□AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )
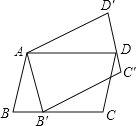
A. 105°B. 170°C. 155°D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B、D、E、F是直线 l上四点,在直线 l的同侧作△ABE和△CDF,且 AB∥CD,∠A=40°.作BG⊥AE于 G,FH⊥CD于 H,BG与 FH交于 P点.
(1)如图 1,B、E、D、F从左至右顺次排列,∠ABD=90°,求∠GPH;
(2)如图 2,B、E、D、F从左至右顺次排列,△ABE与△CDF均为锐角三角形,求∠GPH;
(3)如图 3,F、B、E、D从左至右顺次排列,△ABE为锐角三角形,△CDF为钝角三角形,则∠GPH的度 数为多少?请画出图形并直接写出结果,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
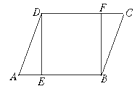
【题目】如图,在平行四边ABCD中,E、F分别是AB、DC上的点,且AE=CF,
(1)求证:△ADE≌△CBF;
(2) 当∠DEB=90°时,试说明四边形DEBF为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
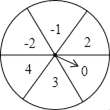
【题目】如图是一个平均被分成6等分的圆,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为x,乙转动转盘后指针所指区域内的数字为y(当指针在边界上时,重转一次,直到指向一个区域为止).
(1)直接写出甲转动转盘后所指区域内的数字为负数的概率;
(2)用树状图或列表法,求出点(x,y)落在第二象限内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com