
【题目】如图1,等腰△ABC中,AC=BC=![]() , ∠ACB=45,AO是BC边上的高,D为线段AO上一动点,以CD为一边在CD下方作等腰△CDE,使CD=CE且∠DCE=45,连结BE.
, ∠ACB=45,AO是BC边上的高,D为线段AO上一动点,以CD为一边在CD下方作等腰△CDE,使CD=CE且∠DCE=45,连结BE.
(1) 求证:△ACD≌△BCE;
(2) 如图2,在图1的基础上,延长BE至Q, P为BQ上一点,连结CP、CQ,若CP=CQ=5,求PQ的长.
(3) 连接OE,直接写出线段OE的最小值.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
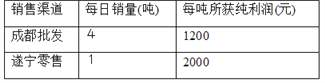
【题目】种植草莓大户张华有22吨草莓待售,现有两种销售渠道:一是运往省城成都直接批发给零售商;二是在遂宁本地市场零售. 经过调查分析,这两种销售渠道每天的销售量以及每吨所获纯利润见下表:
受客观因素和保质期影响,每天只能采用一种销售渠道并且必须在10日内将22吨草莓全部售出.
(1)设将![]() 吨草莓运往成都批发给零售商,其余在遂宁零售,请写出销售完22吨草莓所获纯利润
吨草莓运往成都批发给零售商,其余在遂宁零售,请写出销售完22吨草莓所获纯利润![]() (元)与
(元)与![]() (吨)之间的函数关系式;
(吨)之间的函数关系式;
(2)由于草莓必须在10日内售完,请你求出![]() 的取值范围;
的取值范围;
(3)怎样安排这22吨草莓的销售渠道,才能使所获纯利润最大?并求出最大纯利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]()
![]() 与正比例函数
与正比例函数![]()
![]() 的图象,点A(1,5),点A′(5,b)与点B′均在反比例函数的图象上,点B在直线
的图象,点A(1,5),点A′(5,b)与点B′均在反比例函数的图象上,点B在直线![]() 上,四边形AA′B′B是平行四边形,则B点的坐标为 。
上,四边形AA′B′B是平行四边形,则B点的坐标为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营A种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请用含x的代数式表示该玩具的销售量.
(2)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于450件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
(3)该商场计划将(2)中所得的利润的一部分资金采购一批B种玩具并转手出售,根据市场调查并准备两种方案,方案①:如果月初出售,可获利15%,并可用本和利再投资C种玩具,到月末又可获利10%;方案②:如果只到月末出售可直接获利30%,但要另支付仓库保管费350元,请问商场如何使用这笔资金,采用哪种方案获利较多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.

(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在九(1)班的一次体育测试中,某小组7位女生的一分钟跳绳次数分别是:162,167,158,165,175,142,167,这组数据的中位数是( )
A.156
B.162
C.165
D.167
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题7分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.

(1)选择的条件是 (填序号)
(2)证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,目前我国“神威﹒太湖之光”超级计算机的运算速度位居全球第一,其运算速度达到了每秒1250000000亿次,数字1250000000用科学记数法可简洁表示为( )
A.1.25×109
B.0.125×1010
C.12.5×108
D.1.25×1010
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com