
如图,BD是等边△ABC的高,E是BC延长线上一点,且 .
.

(1)直接写出CE与CD的数量关系;
(2)试说明△BDE是等腰三角形.
(1)CD=CE(2)见解析
【解析】
试题分析:(1)CD=CE,理由为:由等边三角形ABC得到∠ABC为60°,又DB垂直AC,根据“三线合一”得到∠DBC为30°,根据直角三角形中,30°角所对的直角边等于斜边的一半得到CD等于BC的一半,由题中已知的CE等于BC的一半,等量代换可得CD=CE;
(2)由等边三角形ABC得到∠ACB为60°,又(1)得到CD=CE,根据“等边对等角”以及外角性质得到∠E=30°,又∠DBC为30°,故两角相等,再根据“等角对等边”得到BD=DE,即三角形BDE为等腰三角形.
【解析】
(1)CD=CE;(2分)
(2)∵△ABC是等边三角形
∴AB=AC=BC∠ABC=∠ACB=60°,(4分)
∵BD⊥AC
∴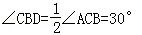 ,
, ,(5分)
,(5分)
∵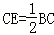
∴CD=CE,(6分)
∴∠E=∠CDE,(7分)
∵∠ACB=∠E+∠CDE
∴ ,(8分)
,(8分)
∴∠CBD=∠E,
∴BD=ED,
∴△BDE是等腰三角形.(9分)


科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上3.1认识不等式1(解析版) 题型:?????
(2006•深圳)下列不等式组的解集,在数轴上表示为如图所示的是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.7探索勾股定理(解析版) 题型:解答题
已知:如图,在△ABC中,∠C=90°,∠B=30°,AC=6,点D在边BC上,AD平分∠CAB,E为AC上的一个动点(不与A、C重合),EF⊥AB,垂足为F.

(1)求证:AD=DB;
(2)设CE=x,BF=y,求y关于x的函数解析式;
(3)当∠DEF=90°时,求BF的长?
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.7探索勾股定理(解析版) 题型:选择题
已知等腰三角形的一条腰长是5,底边长是6,则它底边上的高为( )
A.5 B.3 C.4 D.7
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.7探索勾股定理(解析版) 题型:选择题
如下图,△ABC中,∠C=90°,∠B=45°,AD是角平分线,DE⊥AB于E,则下列结论不正确的是( )

A.AC=AE B.CD=DE C.CD=DB D.AB=AC+CD
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.4等腰三角形的判定定理2(解析版) 题型:解答题
已知:如图,在△ABC中,∠C=90°,AC=BC=4,点M是边AC上一动点(与点A、C不重合),点N在边CB的延长线上,且AM=BN,连接MN交边AB于点P.
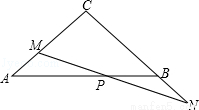
(1)求证:MP=NP;
(2)若设AM=x,BP=y,求y与x之间的函数关系式,并写出它的定义域;
(3)当△BPN是等腰三角形时,求AM的长.
查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.4等腰三角形的判定定理2(解析版) 题型:填空题
如图,AC=BC,∠ACB=90°,AE平分∠BAC,BF⊥AE,交AC延长线于F,且垂足为E,则下列结论:
①AD=BF; ②BF=AF; ③AC+CD=AB,④AB=BF;⑤AD=2BE.
其中正确的结论有 .(填写番号)

查看答案和解析>>
科目:初中数学 来源:2015年课时同步练习(浙教版)八年级上2.4等腰三角形的判定定理1(解析版) 题型:?????
已知a,b,c为△ABC的三边且(a﹣b)(b﹣c)=0,则△ABC为( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com