Question

10．如图，在Rt△ABC中，∠ABC=90°，∠ACD=$\frac{1}{4}$∠ACB，∠ADC=90°，DE⊥AB，若tan∠ACD=$\frac{1}{3}$，AD=$\sqrt{10}$，则2DE+BC=8．

Answer 1

分析 如图，取AC中点O，连接DO，作ON⊥BC于N，延长NO、DE交于点F，作DM⊥AC于M．首先求出AC、DM、OM，tan∠DOM，再证明∠DOM=∠ODE，在Rt△DFO中，求出DF，再证明四边形BNFE是矩形，即可证明2DE+BC=2（DE+BN）=2（DE+EF），延长解决问题．

解答 解：如图，取AC中点O，连接DO，作ON⊥BC于N，延长NO、DE交于点F，作DM⊥AC于M．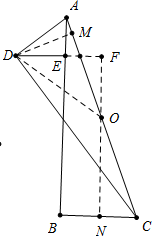

在Rt△ADC中，∵AD=$\sqrt{10}$，tan∠ACD=$\frac{1}{3}$，
∴DC=3AD=3$\sqrt{10}$，AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{（\sqrt{10}）^{2}+（3\sqrt{10}）^{2}}$=10，
∵$\frac{1}{2}$•AD•DC=$\frac{1}{2}$•AC•DM，
∴DM=$\frac{AD•DC}{AC}$=3，
∵AO=OC，
∴DO=OA=OC=5，
∴在Rt△MO中，∵∠DMO=90°，
∴OM=$\sqrt{O{D}^{2}-D{M}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴tan∠DOM=$\frac{3}{4}$，
∵∠ACD=$\frac{1}{4}$∠ACB，
∴∠BCD=3∠DCO，
∵∠DEB=∠B=90°，
∴DE∥CB，
∴∠EDC=∠BCD=3∠ACD，
∵OD=OC，
∴∠ODC=∠ACD，
∴∠EDO=2∠ACD，
∵∠DOM=∠ODC+∠DCA，=2∠ACD，
∴∠EDO=∠DOM，
∴tan∠EDO=tan∠DOM=$\frac{3}{4}$，
∴在Rt△DFO中，tan∠FDO=$\frac{OF}{DF}$=$\frac{3}{4}$，∵DO=5，
∴OF=3，DF=4，
∵∠B=∠FNB=∠FEB=90°，
∴四边形BNFE是矩形，
∴EF=BN，
∵OA=OC，ON∥AB，
∴BN=NC，
∴DE+EF=DE+BN=4，
∴2DE+2BN=8，
∴2DE+BC=8．
故答案为8．

点评 本题考查解直角三角形、勾股定理、锐角三角函数．矩形的判定，平行线的性质等知识，解题的关键是学会添加辅助线，把求2DE+BC的问题转化为求DF，解题的突破点是求出tan∠FDO的值，题目比较难，属于中考填空题中的压轴题．