
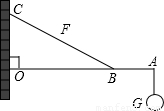
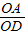 ,则当OD最大时F最小,在Rt△OCB中,用CD表示出OD,为OD2=0.8CD-CD2,由二次函数的性质,可求得OD的最大值,代入数据即可求得最小有力F.
,则当OD最大时F最小,在Rt△OCB中,用CD表示出OD,为OD2=0.8CD-CD2,由二次函数的性质,可求得OD的最大值,代入数据即可求得最小有力F.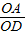 ①.
①.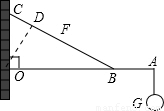
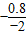 =0.4(m)时,OD最大,
=0.4(m)时,OD最大,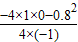 =0.16(m)2,
=0.16(m)2,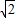 BD=0.4×
BD=0.4×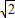 ≈0.57(M).
≈0.57(M).

科目:初中数学 来源: 题型:
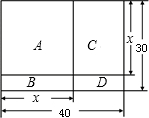 兰花;B.菊花;C.月季;D.牵牛花.且A为正方形.
兰花;B.菊花;C.月季;D.牵牛花.且A为正方形.| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下矩形与原矩形相似,那么剩下矩形的面积是( )
如图所示,长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下矩形与原矩形相似,那么剩下矩形的面积是( )| A、28cm2 | B、27cm2 | C、21cm2 | D、20cm |
查看答案和解析>>
科目:初中数学 来源: 题型:

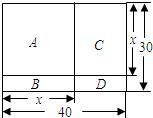
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,长为4cm,宽为3cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上点A位置变化为A→A1→A2,由A1翻滚到A2时被桌面上一小木块挡住,此时长方形木板的边A2C与桌面成30°角,则点A翻滚到A2位置时所经过的路径总长度为
如图所示,长为4cm,宽为3cm的长方形木板在桌面上做无滑动的翻滚(顺时针方向),木板上点A位置变化为A→A1→A2,由A1翻滚到A2时被桌面上一小木块挡住,此时长方形木板的边A2C与桌面成30°角,则点A翻滚到A2位置时所经过的路径总长度为| 7 |
| 2 |
| 7 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com