
ЁОЬтФПЁПЮЊдіЧПбЇЩњЛЗБЃвтЪЖЃЌФГжабЇзщжЏШЋаЃ3000УћбЇЩњВЮМгЛЗБЃжЊЪЖДѓШќЃЌБШШќГЩМЈОљЮЊећЪ§ЃЎДгжаГщШЁВПЗжЭЌбЇЕФГЩМЈНјааЭГМЦЃЌВЂЛцжЦГЩШчЯТЭГМЦЭМЃЎ
ЧыИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉШєГщШЁЕФГЩМЈгУЩШаЮЭМРДУшЪіЃЌдђБэЪОЁАЕкЖўзщЃЈ69.5~79.5ЃЉЁБЕФЩШаЮЕФдВаФНЧ ЖШЃЛ
ЃЈ2ЃЉШєГЩМЈдк90ЗжвдЩЯЃЈКЌ90ЗжЃЉЕФЭЌбЇПЩЛёНБЃЌЧыЙРМЦИУаЃдМгаЖрЩйУћЭЌбЇЛёНБЃП
ЃЈ3ЃЉФГАрзМБИДгГЩМЈзюКУЕФ4УћЭЌбЇЃЈФаЁЂХЎИї2УћЃЉжаЫцЛњбЁШЁ2УћЭЌбЇШЅЩчЧјНјааЛЗБЃаћДЋЃЌдђбЁГіЕФЭЌбЇЧЁКУЪЧ1Фа1ХЎЕФИХТЪЮЊЖрЩйЃП
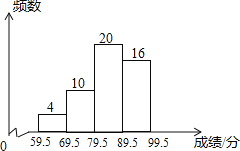
ЁОД№АИЁПЃЈ1ЃЉ72ЁуЃЛЃЈ2ЃЉ960УћЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁПЪдЬтЃЈ1ЃЉгЩЕкШ§зщЃЈ79.5ЁЋ89.5ЃЉЕФШЫЪ§МДПЩЧѓГіЦфЩШаЮЕФдВаФНЧЃЛ
ЃЈ2ЃЉЪзЯШЧѓГі50ШЫжаГЩМЈдк90ЗжвдЩЯЃЈКЌ90ЗжЃЉЕФЭЌбЇПЩвдЛёНБЕФАйЗжБШЃЌНјЖјПЩЙРМЦИУаЃдМгаЖрЩйУћЭЌбЇЛёНБЃЛ
ЃЈ3ЃЉСаБэЕУГіЫљгаЕШПЩФмЕФЧщПіЪ§ЃЌевГібЁГіЕФСНУћжїГжШЫЁАЧЁКУЮЊвЛФавЛХЎЁБЕФЧщПіЪ§ЃЌМДПЩЧѓГіЫљЧѓЕФИХТЪЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩжБЗНЭМПЩжЊЕкШ§зщЃЈ79.5ЁЋ89.5ЃЉЫљеМЕФШЫЪ§ЮЊ20ШЫЃЌ
ЫљвдЁАЕкШ§зщЃЈ79.5ЁЋ89.5ЃЉЁБЕФЩШаЮЕФдВаФНЧ=![]() ЁС360Ёу=144ЁуЃЌ
ЁС360Ёу=144ЁуЃЌ
ЃЈ2ЃЉЙРМЦИУаЃЛёНБЕФбЇЩњЪ§=![]() ЁС2000=640ЃЈШЫЃЉЃЛ
ЁС2000=640ЃЈШЫЃЉЃЛ
ЃЈ3ЃЉСаБэШчЯТЃК

ЫљгаЕШПЩФмЕФЧщПіга12жжЃЌЦфжабЁГіЕФСНУћжїГжШЫЁАЧЁКУЮЊвЛФавЛХЎЁБЕФЧщПіга8жжЃЌдђPЃЈбЁГіЕФСНУћжїГжШЫЁАЧЁКУЮЊвЛФавЛХЎЁБЃЉ=![]() =
=![]() ЃЎЙЪД№АИЮЊЃК
ЃЎЙЪД№АИЮЊЃК ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдке§ЗНаЮ![]() жаЃЌСЌНг
жаЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЮЊЩфЯп
ЮЊЩфЯп![]() ЩЯЕФвЛИіЖЏЕуЃЈгыЕу
ЩЯЕФвЛИіЖЏЕуЃЈгыЕу![]() ВЛжиКЯЃЉЃЌСЌНг
ВЛжиКЯЃЉЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЕФДЙжБЦНЗжЯпНЛЯпЖЮ
ЕФДЙжБЦНЗжЯпНЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() .
.
ЬсГіЮЪЬтЃКЕБЕу![]() дЫЖЏЪБЃЌ
дЫЖЏЪБЃЌ![]() ЕФЖШЪ§ЪЧЗёЗЂЩњИФБфЃП
ЕФЖШЪ§ЪЧЗёЗЂЩњИФБфЃП
ЬНОПЮЪЬтЃК
ЃЈ1ЃЉЪзЯШПМВьЕу![]() ЕФСНИіЬиЪтЮЛжУЃК
ЕФСНИіЬиЪтЮЛжУЃК
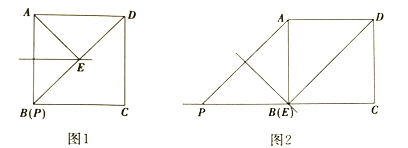
ЂйЕБЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌШчЭМ1ЫљЪОЃЌ
жиКЯЪБЃЌШчЭМ1ЫљЪОЃЌ![]() ____________
____________![]()
ЂкЕБ![]() ЪБЃЌШчЭМ2ЫљЪОЃЌЂйжаЕФНсТлЪЧЗёЗЂЩњБфЛЏЃПжБНгаДГіФуЕФНсТлЃК__________ЃЛЃЈЬюЁАБфЛЏЁБЛђЁАВЛБфЛЏЁБЃЉ
ЪБЃЌШчЭМ2ЫљЪОЃЌЂйжаЕФНсТлЪЧЗёЗЂЩњБфЛЏЃПжБНгаДГіФуЕФНсТлЃК__________ЃЛЃЈЬюЁАБфЛЏЁБЛђЁАВЛБфЛЏЁБЃЉ
ЃЈ2ЃЉШЛКѓПМВьЕу![]() ЕФвЛАуЮЛжУЃКвРЬтвтВЙШЋЭМ3ЃЌЭМ4ЃЌЭЈЙ§ЙлВьЁЂВтСПЃЌЗЂЯжЃКЃЈ1ЃЉжаЂйЕФНсТлдквЛАуЧщПіЯТ_________ЃЛЃЈЬюЁАГЩСЂЁБЛђЁАВЛГЩСЂЁБЃЉ
ЕФвЛАуЮЛжУЃКвРЬтвтВЙШЋЭМ3ЃЌЭМ4ЃЌЭЈЙ§ЙлВьЁЂВтСПЃЌЗЂЯжЃКЃЈ1ЃЉжаЂйЕФНсТлдквЛАуЧщПіЯТ_________ЃЛЃЈЬюЁАГЩСЂЁБЛђЁАВЛГЩСЂЁБЃЉ
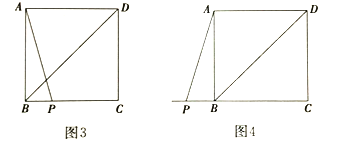
ЃЈ3ЃЉжЄУїВТЯыЃКШєЃЈ1ЃЉжаЂйЕФНсТлдквЛАуЧщПіЯТГЩСЂЃЌЧыДгЭМ3КЭЭМ4жаШЮбЁвЛИіНјаажЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() БпЩЯвЛЕуЃЌСЌНг
БпЩЯвЛЕуЃЌСЌНг![]() ЃЌАб
ЃЌАб![]() би
би![]() елЕўЃЌЪЙЕу
елЕўЃЌЪЙЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌЕБ
ДІЃЌЕБ![]() ЮЊжБНЧШ§НЧаЮЪБЃЌ
ЮЊжБНЧШ§НЧаЮЪБЃЌ![]() ЕФГЄЮЊЃЈ ЃЉ
ЕФГЄЮЊЃЈ ЃЉ
A. 3B. ![]() C. 2Лђ3D. 3Лђ
C. 2Лђ3D. 3Лђ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЃЌГЄЗНаЮ![]() ЕФШ§ИіЖЅЕуЕФзјБъЮЊ
ЕФШ§ИіЖЅЕуЕФзјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() жсЃЌЕу
жсЃЌЕу![]() ЪЧГЄЗНаЮФквЛЕуЃЈВЛКЌБпНчЃЉ.
ЪЧГЄЗНаЮФквЛЕуЃЈВЛКЌБпНчЃЉ.

ЃЈ1ЃЉЧѓ![]() ЃЌ
ЃЌ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ЃЈ2ЃЉШєНЋЕу![]() ЯђзѓвЦЖЏ8ИіЕЅЮЛЃЌдйЯђЩЯвЦЖЏ2ИіЕЅЮЛЕНЕу
ЯђзѓвЦЖЏ8ИіЕЅЮЛЃЌдйЯђЩЯвЦЖЏ2ИіЕЅЮЛЕНЕу![]() ЃЌШєЕу
ЃЌШєЕу![]() ЧЁКУгыЕу
ЧЁКУгыЕу![]() Йигк
Йигк![]() жсЖдГЦЃЌЧѓ
жсЖдГЦЃЌЧѓ![]() ЃЌ
ЃЌ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк20kmдНвАШќжаЃЌМзввСНбЁЪжЕФааГЬyЃЈЕЅЮЛЃКkmЃЉЫцЪБМфxЃЈЕЅЮЛЃКhЃЉБфЛЏЕФЭМЯѓ
ШчЭМЫљЪОЃЌИљОнЭМжаЬсЙЉЕФаХЯЂЃЌгаЯТСаЫЕЗЈЃК
ЂйСНШЫЯргіЧАЃЌМзЕФЫйЖШаЁгкввЕФЫйЖШЃЛ ЂкГіЗЂКѓ1аЁЪБЃЌСНШЫааГЬОљЮЊ10kmЃЛ
ЂлГіЗЂКѓ1.5аЁЪБЃЌМзЕФааГЬБШввЖр3kmЃЛ ЂмМзБШввЯШЕНДяжеЕуЃЎ
Цфжае§ШЗЕФгаЃЈ ЃЉ

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
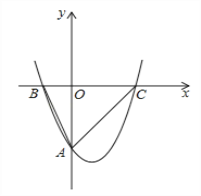
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯп![]() гыyжсНЛгкЕуAЃЈ0ЃЌЉ4ЃЉЃЌгыxжсЯрНЛгкBЃЈЉ2ЃЌ0ЃЉЁЂCЃЈ4ЃЌ0ЃЉСНЕуЃЌOЮЊзјБъдЕуЃЎ
гыyжсНЛгкЕуAЃЈ0ЃЌЉ4ЃЉЃЌгыxжсЯрНЛгкBЃЈЉ2ЃЌ0ЃЉЁЂCЃЈ4ЃЌ0ЃЉСНЕуЃЌOЮЊзјБъдЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕуEдкxжсЩЯЃЌЁЯOEA+ЁЯOAB=ЁЯACBЃЌЧѓBEЕФГЄЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌНЋХзЮяЯпy=ax2+bx+cЯђгвЦНвЦnЃЈnЃО0ЃЉИіЕЅЮЛЕУЕНЕФаТХзЮяЯпгыxжсНЛгкMЁЂNЃЈMдкNзѓВрЃЉЃЌPЮЊxжсЯТЗНЕФаТХзЮяЯпЩЯШЮвтвЛЕуЃЌСЌPMЁЂPNЃЌЙ§PзїPQЁЭMNгкQЃЌ![]() ЪЧЗёЮЊЖЈжЕЃПЧыЫЕУїРэгЩЃЎ
ЪЧЗёЮЊЖЈжЕЃПЧыЫЕУїРэгЩЃЎ
ЭМ1 ЭМ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2019Фъ2дТЃЌЪаГЧЧјЙЋНЛГЕЪЉааШЋГЬУтЗбГЫзјеўВпЃЌБъжОзХЮвЪаЙЋЙВНЛЭЈНЈЩшТѕНјСЫвЛИіаТЕФЪБДњЃЎЯТЭМЮЊФГвЛЬѕЖЋЮїЗНЯђжБЯпЩЯЕФЙЋНЛЯпТЗЃЌЖЋЦ№жАНЬдАЧјеОЃЌЮїжСИЛЪППЕеОЃЌЭОжаЙВЩш![]() ИіЩЯЯТГЕеОЕуЃЌШчЭМЫљЪО:
ИіЩЯЯТГЕеОЕуЃЌШчЭМЫљЪО:
ФГЬьЃЌаЁЭѕДгЕчвЕОжеОГіЗЂЃЌЪМжедкИУЯпТЗЕФЙЋНЛеОЕузіжОдИепЗўЮёЃЌЕН![]() еОЯТГЕЪБЃЌБОДЮжОдИепЗўЮёЛюЖЏНсЪјЃЌШчЙћЙцЖЈЯђЖЋЮЊе§ЃЌЯђЮїЮЊИКЃЌЕБЬьЕФГЫГЕеОЪ§АДЯШКѓЫГађвРДЮМЧТМШчЯТ(ЕЅЮЛ:еО):
еОЯТГЕЪБЃЌБОДЮжОдИепЗўЮёЛюЖЏНсЪјЃЌШчЙћЙцЖЈЯђЖЋЮЊе§ЃЌЯђЮїЮЊИКЃЌЕБЬьЕФГЫГЕеОЪ§АДЯШКѓЫГађвРДЮМЧТМШчЯТ(ЕЅЮЛ:еО): ![]() ЃЛ
ЃЛ
![]() ЧыЭЈЙ§МЦЫуЫЕУї
ЧыЭЈЙ§МЦЫуЫЕУї![]() еОЪЧФФвЛеОЃП
еОЪЧФФвЛеОЃП
![]() ШєЯрСкСНеОжЎМфЕФЦНОљОрРыЮЊ
ШєЯрСкСНеОжЎМфЕФЦНОљОрРыЮЊ![]() ЧЇУзЃЌЧѓетДЮаЁЭѕжОдИЗўЮёЦкМфГЫзјЙЋНЛГЕааНјЕФзмТЗГЬЪЧЖрЩйЧЇУзЃП
ЧЇУзЃЌЧѓетДЮаЁЭѕжОдИЗўЮёЦкМфГЫзјЙЋНЛГЕааНјЕФзмТЗГЬЪЧЖрЩйЧЇУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгавЛжжНкФмаЭНЮГЕЕФгЭЯфМгТњЬьШЛЦјКѓЃЌгЭЯфжаЕФЪЃгрЬьШЛЦјСП![]() ЃЈЩ§ЃЉгыНЮГЕааЪЛТЗГЬ
ЃЈЩ§ЃЉгыНЮГЕааЪЛТЗГЬ![]() ЃЈЧЇУзЃЉжЎМфЕФЙиЯЕШчЭМЫљЪОЃЌИљОнЭМЯѓЛиД№ЯТСаЮЪЬтЃК
ЃЈЧЇУзЃЉжЎМфЕФЙиЯЕШчЭМЫљЪОЃЌИљОнЭМЯѓЛиД№ЯТСаЮЪЬтЃК
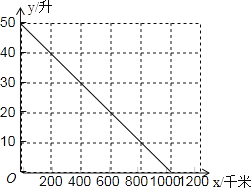
ЃЈ1ЃЉетжжНЮГЕЕФгЭЯфзюЖрФмзА______Щ§ЬьШЛЦјЃЌМгТњЬьШЛЦјКѓПЩЙЉНЮГЕааЪЛ______ЧЇУз.
ЃЈ2ЃЉНЮГЕУПааЪЛ200ЧЇУзЯћКФЬьШЛЦј________Щ§.
ЃЈ3ЃЉаДГі![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪН.
жЎМфЕФКЏЪ§ЙиЯЕЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
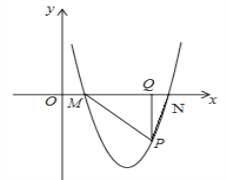
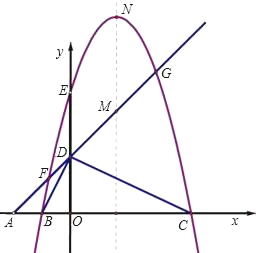
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌЕуAЁЂBЁЂCдкxжсЩЯЃЌЕуDЁЂEдкyжсЩЯЃЌOA=OD=2ЃЌOC=OE=4ЃЌBЮЊЯпЖЮOAЕФжаЕуЃЌжБЯпADгыОЙ§BЁЂEЁЂCШ§ЕуЕФХзЮяЯпНЛгкFЁЂGСНЕуЃЌгыЦфЖдГЦжсНЛгкMЃЌЕуPЮЊЯпЖЮFGЩЯвЛИіЖЏЕуЃЈгыFЁЂGВЛжиКЯЃЉЃЌPQЁЮyжсгыХзЮяЯпНЛгкЕуQЃЎ
ЃЈ1ЃЉЧѓОЙ§BЁЂEЁЂCШ§ЕуЕФХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉХаЖЯЁїBDCЕФаЮзДЃЌВЂИјГіжЄУїЃЛЕБPдкЪВУДЮЛжУЪБЃЌвдPЁЂOЁЂCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌВЂЧѓГіДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШєХзЮяЯпЕФЖЅЕуЮЊNЃЌСЌНгQNЃЌЬНОПЫФБпаЮPMNQЕФаЮзДЃКЂйФмЗёГЩЮЊСтаЮЃЛЂкФмЗёГЩЮЊЕШбќЬнаЮЃПШєФмЃЌЧыжБНгаДГіЕуPЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com