
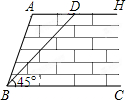
 如图,某拦河坝截面的原设计方案为:坝高为6m,坡角∠ABC=60°.为了提高拦河坝的安全性,现将坡角改为45°,由此,点A需向右平移至点D,求AD的长.(参考数据:
如图,某拦河坝截面的原设计方案为:坝高为6m,坡角∠ABC=60°.为了提高拦河坝的安全性,现将坡角改为45°,由此,点A需向右平移至点D,求AD的长.(参考数据:| 3 |
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
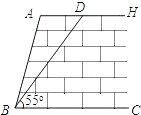 如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC=74°,坝顶到坝脚的距离AB=6m.为了提高拦河坝的安全性,现将坡角改为55°,由此,点A需向右平移至点D,请你计算AD的长.(精确到0.1m)
如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC=74°,坝顶到坝脚的距离AB=6m.为了提高拦河坝的安全性,现将坡角改为55°,由此,点A需向右平移至点D,请你计算AD的长.(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:
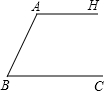 安全性,现将坡角改为45°,为此,点A需向右平移至点D.
安全性,现将坡角改为45°,为此,点A需向右平移至点D.查看答案和解析>>
科目:初中数学 来源: 题型:
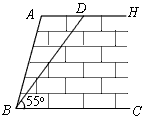
 如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC=60°,坝顶到坝脚的距离AB=6m.为了提高拦河坝的安全性,现将坡角改为45°,由此,点A需向右平移至点D,请你计算AD的长(精确到0.1m).
如图,某拦河坝截面的原设计方案为:AH∥BC,坡角∠ABC=60°,坝顶到坝脚的距离AB=6m.为了提高拦河坝的安全性,现将坡角改为45°,由此,点A需向右平移至点D,请你计算AD的长(精确到0.1m).查看答案和解析>>
科目:初中数学 来源:贵州省中考真题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com