
【题目】如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.


【答案】见解析
【解析】分析:(1)用三角形的内角和定理判断∠D+∠B=180°;(2)连接EC,证明∠AEC+∠ACE+∠3+∠4=180°,根据同旁内角互补,两直线平行证明.
详解:(1)∵∠1=∠3,∠2=∠4,∴∠1+∠3+∠2+∠4=2(∠1+∠2),
∵∠1+∠2=90°,∴∠1+∠3+∠2+∠4=180°;
∵∠D+∠B+∠1+∠3+∠2+∠4=360°,∴∠D+∠B=180°,
∴DE∥BC.
(2)成立.
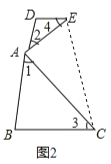
如图2,连接EC;
∵∠1=∠3,∠2=∠4,且∠1+∠2=90°,∴∠3+∠4=∠1+∠2=90°;
∵∠EAC=90°,∴∠AEC+∠ACE=180°-90°=90°,
∴∠AEC+∠ACE+∠3+∠4=180°,
∴DE∥BC,
即(1)中的结论仍成立.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为________________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
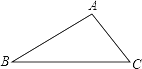
【题目】已知:如图,在△ABC中,∠B=30°,∠C=45°,AC=2![]() ,
,
求:(1)AB的长为________;
(2)S△ABC=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.其中正确的结论的个数有( )个.

A.5 B.4 C.3 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(﹣3,﹣2)、B(﹣1,﹣4)
(1)直接写出:S△OAB= ;
(2)延长AB交y轴于P点,求P点坐标;
(3)Q点在y轴上,以A、B、O、Q为顶点的四边形面积为6,求Q点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把三角形ABC向上平移3个单位长度,再向右平移2个单位长度,得到三角形A1B1C1.
(1)在图中画出三角形A1B1C1;
(2)写出点A1,B1的坐标;
(3)在y轴上是否存在一点P,使得三角形BCP与三角形ABC面积相等?若存在,请直接写出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=3x2﹣6x+k(k为常数)的图像经过点A(0.8,y1),B(1.1,y2),C( ![]() ,y3),则有( )
,y3),则有( )
A.y1<y2<y3
B.y1>y2>y3
C.y3>y1>y2
D.y1>y3>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将下列证明过程补充完整:
已知:如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2
求证:∠E=∠F

证明:∵∠BAP+∠APD=180°(已知)
∴ ∥ ( )
∴∠BAP= ( )
又∵∠1=∠2(已知)
∴∠BAP﹣ = ﹣∠2
即∠3= (等式的性质)
∴AE∥PF( )
∴∠E=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,是不可能事件的是
A.买一张电影票,座位号是奇数 B.射击运动员射击一次,命中9环
C.明天会下雨 D.度量三角形的内角和,结果是360°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com