

���� ��1�����������C�����꣬Ȼ�����ô���ϵ������������ߵĽ���ʽ��
��2����P��CD�����P��CD��������������ۿɵ�y��m֮��ĺ�����ϵʽ��
��3�����ʷ��������ĵ�P��2�������ͼ2��ʾ��ע�ⲻҪ©�⣮�����P�����ʱ����Ҫ����ھ���֪����������ֱ�������λ����������Σ��ⷽ�������P�����꣮
���  �⣺��1����x=0ʱ��y=2����C��0��2����
�⣺��1����x=0ʱ��y=2����C��0��2����
��C��0��2����D��-3��$\frac{7}{2}$���������ʽy=-x2+bx+c�ã�$\left\{\begin{array}{l}c=2\\-9-3b+c=\frac{7}{2}\end{array}\right.$
���$\left\{\begin{array}{l}c=2\\ b=-\frac{7}{2}\end{array}\right.$����y=-x2-$\frac{7}{2}$x+2��
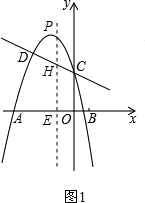
��2����P��CD���棬��ͼ1����P������Ϊ��m��-m2-$\frac{7}{2}$m+2������F������Ϊ��m��-$\frac{1}{2}$m+2����
�߶�PH�ij���Ϊd=-m2-$\frac{7}{2}$m+2+$\frac{1}{2}$m-2=-m2-3m��-4��m��0����
��P��CD���棬��ͼ2����P������Ϊ��m��-m2-$\frac{7}{2}$m+2������H������Ϊ��m��-$\frac{1}{2}$m+2����
�߶�PH�ij���Ϊd=-$\frac{1}{2}$m+2+m2+$\frac{7}{2}$m-2=m2+3m��-4��m��-3����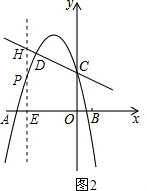
��3�����ڣ�
���ɣ�����ͼ4��ʾ������C��CM��PE�ڵ�M����CM=-m��EM=2��
��HM=yH-EM=-$\frac{1}{2}$m��
��tan��CHM=2��
��Rt��CHM�У��ɹ��ɶ����ã�CH=-$\frac{\sqrt{5}}{2}$m������P��PN��CD�ڵ�N����PN=HN•tan��PHN=HN•tan��CHM=2HN��
�ߡ�PCH=45�㣬
��PN=CN��
��PN=2HN
��HN=CH=-$\frac{\sqrt{5}}{2}$m��PN=2HN=-$\sqrt{5}$m��
��Rt��PHN�У��ɹ��ɶ����ã�PH=$\sqrt{{HN}^{2}+{PN}^{2}}$=-$\frac{5}{2}$m��
��PH=yP-yH=��-m2-$\frac{7}{2}$m+2��-��-$\frac{1}{2}$m+2��=-m2-3m��
��-m2-3m=-$\frac{5}{2}$m�������ã�m2+$\frac{1}{2}$m=0��
���m=0����ȥ����m=-$\frac{1}{2}$��
��P��-$\frac{1}{2}$��$\frac{7}{2}$����
����ͼ5��ʾ������C��CM��PE�ڵ�M����CM=-m��EM=2��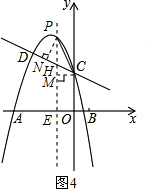
��HM=yH-EM=-$\frac{1}{2}$m��
��tan��CHM=2��
��Rt��CHM�У��ɹ��ɶ����ã�CH=-$\frac{\sqrt{5}}{2}$m������P��PN��CD�ڵ�N����PN=HN•an��PHN=HN•tan��CHM=2HN��
�ߡ�PCH=45�㣬
��PN=CN��
��PN=2HN��
��HN=$\frac{1}{3}$CH=-$\frac{\sqrt{5}}{6}$m��PN=2HN=-$\frac{\sqrt{5}}{3}$m��
��Rt��PHN�У��ɹ��ɶ����ã�PH=$\sqrt{{HN}^{2}+{PN}^{2}}$=-$\frac{5}{6}$m��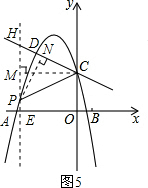
��PH=yH-yP=��-$\frac{1}{2}$m+2��-��-m2-$\frac{7}{2}$m+2��=m2+3m��
��m2+3m=-$\frac{5}{6}$m�������ã�m2+$\frac{23}{6}$m=0��
���m=0����ȥ����m=-$\frac{23}{6}$��
��P��-$\frac{23}{6}$��$\frac{13}{18}$����
�ʵ�P����ΪP��-$\frac{1}{2}$��$\frac{7}{2}$����P��-$\frac{23}{6}$��$\frac{13}{18}$����
���� ���⿼���˶��κ����ۺ��⣬�����ʽҪ�ô���ϵ��������d�Ľ�������ʽҪ����һ�κ�������κ����IJ��г���ʽ������Ҫ��ע��3������3���Ǵ��������⣬Ҫע��������ۣ�������ȷͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
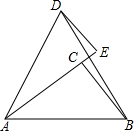 ��ͼ����ABDΪ�ȱ������Σ���ACBΪ�����������ҡ�ACB=90�㣬DE��AC��AC���ӳ����ڵ�E����֤��DE=CE��
��ͼ����ABDΪ�ȱ������Σ���ACBΪ�����������ҡ�ACB=90�㣬DE��AC��AC���ӳ����ڵ�E����֤��DE=CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
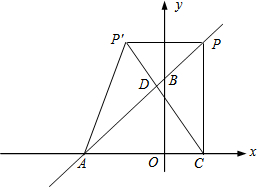 ��ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬��A�������ǣ�-6��0������B�������ǣ�0��n����n��0����P��ֱ��AB�ϵ�һ�����㣬��PC��x�ᣬ����ΪC���ǵ�P����y��ĶԳƵ�ΪP�䣨��P�䲻��y���ϣ�������PP�䣬P��A��P��C�����P�ĺ�����Ϊm��
��ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬��A�������ǣ�-6��0������B�������ǣ�0��n����n��0����P��ֱ��AB�ϵ�һ�����㣬��PC��x�ᣬ����ΪC���ǵ�P����y��ĶԳƵ�ΪP�䣨��P�䲻��y���ϣ�������PP�䣬P��A��P��C�����P�ĺ�����Ϊm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��2��4 | B�� | 6��3��6 | C�� | 4��4��5 | D�� | 1��1��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ������ˮ��߶�Ϊ5m�İ���C������������������������ʼʱ����CB��ˮ��AB�ļн�Ϊ30�㣬������ÿ��0.5m���ٶ����������ӣ�8s�������˵�D��λ�ã��ʴ����ƶ��˶����ף�
��ͼ��ʾ������ˮ��߶�Ϊ5m�İ���C������������������������ʼʱ����CB��ˮ��AB�ļн�Ϊ30�㣬������ÿ��0.5m���ٶ����������ӣ�8s�������˵�D��λ�ã��ʴ����ƶ��˶����ף��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com