
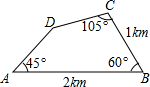
 为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )
为测出所住小区的面积,某人进行了一些测量工作,所得数据如图所示,则小区的面积是( )| A. | $\frac{3+\sqrt{6}}{4}$km2 | B. | $\frac{3-\sqrt{6}}{4}$km2 | C. | $\frac{6+\sqrt{3}}{4}$km2 | D. | $\frac{6-\sqrt{3}}{4}$km2 |
分析 把图形切割成规则的几何图形,然后计算出不规则小区的面积.
解答  解:过点D做DE⊥AB,垂足为E,过点C做CF⊥AB,垂足为F,过点D做DG⊥CF,垂足为G.
解:过点D做DE⊥AB,垂足为E,过点C做CF⊥AB,垂足为F,过点D做DG⊥CF,垂足为G.
设AE的长为xkm.
在Rt△AED中,由于∠A=45°,所以DE=AE=xkm.
在Rt△BCF中,由于∠B=60°,BC=1,所以∠BCF=30°,BF=$\frac{1}{2}$,CF=$\frac{\sqrt{3}}{2}$.
在Rt△CGD中,由于∠DCG=105°-30°=75°,所以∠CDG=15°.
在矩形DEFG中,EF=DG=$\frac{3}{2}-a$,DE=FG=xkm,CG=CF-GF=$\frac{\sqrt{3}}{2}$-a.
在Rt△CGD中,tan∠CDG=$\frac{CG}{DG}$,即tan15°=$\frac{\frac{\sqrt{3}}{2}-a}{\frac{3}{2}-a}$
因为tan15°=2-$\sqrt{3}$,所以$\frac{\sqrt{3}}{2}-a=(2-\sqrt{3})(\frac{3}{2}-a)$
解得:a=$\frac{3-\sqrt{3}}{2}$
S小区=S△AED+S梯形DEFC+S△CFB
=$\frac{1}{2}$a2+$\frac{1}{2}$(a+$\frac{\sqrt{3}}{2}$)($\frac{3}{2}$-a)+$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$
=$\frac{1}{2}$($\frac{3-\sqrt{3}}{2}$)2+$\frac{1}{2}$×$\frac{3}{2}$×$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$
=$\frac{6-\sqrt{3}}{4}$.
故选D.
点评 本题考查了直角三角形的面积和梯形的面积及根式的加减,解决本题的关键是把不规则的四边形切割成直角三角形和梯形,充分利用特殊角60°和45°..


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
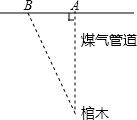 如图,一个古代棺木被探明位于A点地下24米处,由于A点地面下有煤气管道,考古人员下能垂直向下挖掘,他们被允许从距A点8米的B点挖掘,考占人员应以与地平面形成多大的角度进行挖掘才能沿最短路线挖到棺木?他们需要挖多长的距离?
如图,一个古代棺木被探明位于A点地下24米处,由于A点地面下有煤气管道,考古人员下能垂直向下挖掘,他们被允许从距A点8米的B点挖掘,考占人员应以与地平面形成多大的角度进行挖掘才能沿最短路线挖到棺木?他们需要挖多长的距离?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
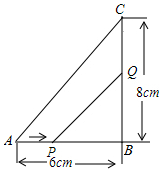 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).
如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿A边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com