
如图,菱形ABCD中,AC=8,BD=6,将△ABD沿AC方向向右平移到△A′B′D′的位置,若平移距离为2,则阴影部分的面积为_________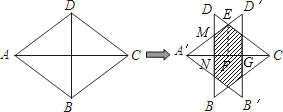
7.5.
解析试题分析:首先设A′D′交CD于点E,交BD于点M,BD交A′C于点N,过点E作EF⊥A′C于点F,由平移的性质与菱形的性质,易求得A′G,A′N,A′F与D′G的长,易得BD∥EF∥B′D′,即可求得△A′MN∽△A′D′G,△A′EF∽△A′D′G,然后由相似三角形的对应边成比例,即可求得MN与EF的长,继而求得梯形MNFE的面积,则可求得答案.
试题解析:根据题意得:NG=2,
设A′D′交CD于点E,交BD于点M,BD交A′C于点N,过点E作EF⊥A′C于点F,
由平移的性质可得:NF=GF= NG=1,
NG=1,
∵菱形ABCD中,AC=8,BD=6,
∴A′G= AC=4,D′G=
AC=4,D′G= BD=3,B′D′⊥A′C,BD⊥A′C,
BD=3,B′D′⊥A′C,BD⊥A′C,
∴A′N-A′G=NG=4-2=2,A′F=A′G-GF=4-1=3,BD∥EF∥B′D′,
∴△A′MN∽△A′D′G,△A′EF∽△A′D′G,
∴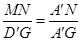 ,
,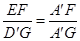 ,
,
即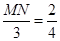 ,
,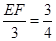 ,
,
∴MN= ,EF=
,EF=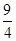 ,
,
∴S梯形MNFE= ×(MN+EF)×HF=
×(MN+EF)×HF= ×(
×( +
+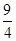 )×1=
)×1=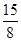 ,
,
∴S阴影=4S梯形MNFE=4×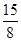 =7.5.
=7.5.
考点:1.相似三角形的判定与性质;2.菱形的性质;3.平移的性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:单选题
如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有
A.1条 B.2条 C.3条 D.4条
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连接PA.设PA=x,PB=y,则(x-y)的最大值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②  ;③△PMN为等边三角形; ④当∠ABC=45°时,BN=
;③△PMN为等边三角形; ④当∠ABC=45°时,BN= PC.其中正确的是__________.
PC.其中正确的是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com