
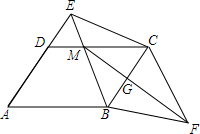
 如图所示,点M是平行四边形ABCD的边CD上一点,且DM:MC=1:2,四边形EBFC为平行四边形,FM与BC交于点G.若三角形FCG的面积与三角形MED的面积之差为13cm2,平行四边形ABCD的面积是60cm2.
如图所示,点M是平行四边形ABCD的边CD上一点,且DM:MC=1:2,四边形EBFC为平行四边形,FM与BC交于点G.若三角形FCG的面积与三角形MED的面积之差为13cm2,平行四边形ABCD的面积是60cm2. 分析 记△DEM面积为S,则易知△EMC面积为2S,△BMC面积为4S,△BCF面积为6S,由BE∥CF,BE=CF,得$\frac{BM}{CF}$=$\frac{BG}{GC}$=$\frac{2}{3}$,推出△FGC的面积为$\frac{18}{5}$S,列出方程即可解决问题.
解答 解:如图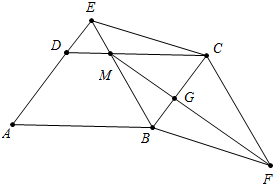 记△DEM面积为S,
记△DEM面积为S,
∵四边形ABCD是平行四边形,
∴AE∥BC,
∴$\frac{DM}{MC}$=$\frac{EM}{BM}$=$\frac{1}{2}$,
∴△EMC面积为2S,△MCG面积为4S,
∵四边形EBFC为平行四边形,
∴BE∥CF,BE=CF,
∴$\frac{BM}{CF}$=$\frac{BG}{GC}$=$\frac{2}{3}$,
∵S△BCE=S△BCF=6S,
∴S△FGC=$\frac{3}{5}$S△BFC=$\frac{18}{5}$S,
由题意:$\frac{18}{5}$S-S=13,
∴S=5,
∴S平行四边形ABCD=2S△EBC=12S=60cm2.
故答案为60.
点评 本题考查平行四边形的性质、平行线分线段成比例定理、异底同高的三角形面积比等于底的比,学会设参数解决问题,属于中考常考题型.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
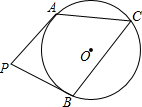 如图,PA,PB分别与⊙O相切于A,B两点,sin∠C=$\frac{4}{5}$,PA=$\frac{20}{3}$,则⊙O的面积为( )
如图,PA,PB分别与⊙O相切于A,B两点,sin∠C=$\frac{4}{5}$,PA=$\frac{20}{3}$,则⊙O的面积为( )| A. | 16π | B. | 25π | C. | 9π | D. | 8π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )
在直线y=-x+4032的图象上有点P1、P2、P3…、P2014,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1、P2、P3…、P2014分别作x轴、y轴的垂线段,构成若干个长方形,如图所示,将图中阴影部分的面积从左至右依次记为S1、S2、S3…、S2014,则S1+S2+S3…+S2014=( )| A. | 8056 | B. | 8050 | C. | 8054 | D. | 8052 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△A1OB1是边长为1的等边三角形,将其以原点O为中心在原点两侧进行位似变换,得△A2OB2,二者的位似比为1:2,将△A2OB2以x轴为对称轴进行轴对称变换,得△A3OB2再原点O为中心在原点两侧进行位似变换,得△A4OB3,二者的位似比为1:2,按此规律.则点A2016的坐标为($\frac{1}{2}$×4504,$\frac{\sqrt{3}}{2}$×4504).
如图,△A1OB1是边长为1的等边三角形,将其以原点O为中心在原点两侧进行位似变换,得△A2OB2,二者的位似比为1:2,将△A2OB2以x轴为对称轴进行轴对称变换,得△A3OB2再原点O为中心在原点两侧进行位似变换,得△A4OB3,二者的位似比为1:2,按此规律.则点A2016的坐标为($\frac{1}{2}$×4504,$\frac{\sqrt{3}}{2}$×4504).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com